Pensamos en las partículas fundamentales como algo muy pequeño, pero los neutrinos “vestigiales” del Big Bang podrían ser grandes. Realmente grandes. Según un artículo aparecido el 22 de mayo en Physical Review Letters, la onda mecanocuántica asociada a uno solo de ellos podría tener un tamaño de miles de millones de años luz de largo, un buen porcentaje del universo observable [1]. Una onda tan grande suscita preguntas acerca de como una partícula cuántica interacciona con la gravedad de galaxias y cúmulos de galaxias; preguntas que no tienen aún respuestas.
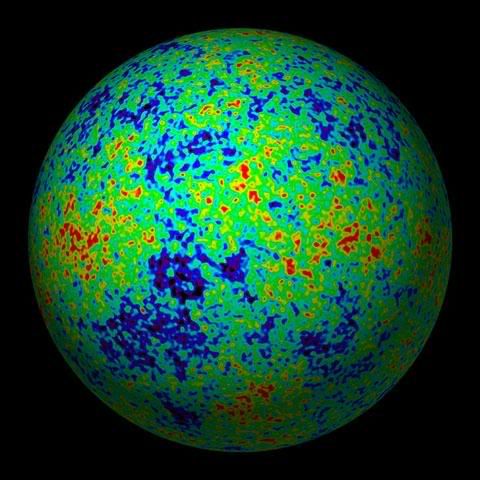
Los neutrinos vestigiales, como los fotones vestigiales que constituyen la radiación de fondo de microondas [en la imagen], son residuos del universo caliente y denso de hace 13.700 millones de años. Si bien la densidad de partículas ha descendido muchísimo conforme el universo se expandía, y lo sigue haciendo, todavía quedan poco más o menos 300 neutrinos vestigiales por cada centímetro cúbico, casi lo mismo que fotones vestigiales. La energía media también ha descendido a lo largo del tiempo a un valor tan bajo que los neutrinos vestigiales son completamente indetectables por los observatorios terrestres.
Los neutrinos oscilan entre tres “sabores” cuando se mueven por el espacio, y cada estado correspondiente a un sabor es una combinación de tres estados de masa. La masa precisa de estos estados aún no se conoce, pero los investigadores han establecido límites a los valores que puede adoptar. Los estados de masa son algo así como los “colores primarios”, los neutrinos, como el resto de colores, son una combinación de ellos. George Fuller y Chad Kishimoto, de la Universidad de California en San Diego (EE.UU.), querían comprobar si el límite teórico superior calculado para las masas de los neutrinos basado en las observaciones de galaxias se vería afectado si se tenía en cuenta la oscilación entre sabores. La respuesta fue que no, al menos para el nivel de precisión que tienen las mediciones actuales.
Al hacer sus cálculos los físicos se encontraron con algo inesperado relacionado con las funciones de onda de los neutrinos, con la dualidad onda-partícula en mecánica cuántica no relativista.
La dualidad onda-partícula esta profundamente arraigada en los fundamentos de la mecánica cuántica. Así, la teoría establece que toda la información de la partícula está codificada en su función de onda, una función compleja que viene a ser análoga a la amplitud de la onda en cada punto del espacio. Esta función de onda cambia según una ecuación diferencial, la famosa ecuación de Schrödinger, que explica los comportamientos ondulatorios asociados a la partícula, como la interferencia o la difracción.
El comportamiento de partícula se hace más evidente en los fenómenos asociados a la medición en mecánica cuántica. En el momento en que se mide la localización de una partícula, la función de onda colapsará al azar a una función de valores concretos para cada localización posible, siendo estos valores la probabilidad de cada una, y ésta igual al cuadrado de la amplitud en ese punto. Por lo tanto la medición dará una localización bien definida (una nube de probabilidad), una propiedad asociada con las partículas.
Fuller y Kishimoto encontraron que las funciones de onda de los neutrinos vestigiales podían abarcar miles de millones de años luz. La mitad de la función de onda de un neutrino podría estar, por ejemplo, en nuestra galaxia y la otra al borde del universo observable. Esto sería consecuencia de la combinación de los estados de masa que constituyen cada neutrino. Cada estado de masa por si mismo viajaría a diferente velocidad, más lento cuanto más masa. A los niveles de energía habituales de los neutrinos estas velocidades estarían todas muy próximas a la velocidad de la luz. Pero los neutrinos vestigiales tienen una energía muy baja. Tan baja que la velocidad intrínseca del estado con mayor masa podría ser mucho menor que la velocidad de la luz, mientras que los otros dos seguirían estando próximos a c. Lo suficientemente menor como para que sea de aplicación la mecánica cuántica no relativista que comentábamos antes.
¿Qué pasa entonces cuando el neutrino viaja a través de una galaxia y va tan lento que puede ser atrapado por el campo gravitatorio? ¿Podría esto considerarse una “medición”? Hemos visto que al medir colapsamos la función de onda, ¿significa esto que la función de onda colapsa por el efecto del campo gravitatorio o simplemente se distorsiona? Las respuestas a estas y otras preguntas todavía son objeto de debate [2].
Referencias:
[1]
Fuller, G., & Kishimoto, C. (2009). Quantum Coherence of Relic Neutrinos Physical Review Letters, 102 (20) DOI: 10.1103/PhysRevLett.102.201303
[2]
Christian, J. (2005). Testing Gravity-Driven Collapse of the Wave Function via Cosmogenic Neutrinos Physical Review Letters, 95 (16) DOI: 10.1103/PhysRevLett.95.160403

si hemos dicho que la energia que tienen es muy baja, hemos dicho que cuando mas lento menos masa, asi que a mas velocidad mas masa?
ResponderEliminarno puede ser eso, choca con
E=mc2
porque no puede haber mecanica cuantica no relativista.
mmmmmm......
Por casualidad he caído en esta entrada, y tengo que decir que el título no es correcto. Dice el abstract que lo que es grande es el "paquete de ondas" ("wave packet").
ResponderEliminarLa mecánica cuántica es de naturaleza probabilística, y aunque no podamos definir exactamente dónde está una partícula, podemos dar una probabilidad a cada punto del espacio de que esté ahí. Por ejemplo, si metemos a un electrón dentro de una caja cerrada, no podremos decir dónde está, pero casi seguro que se encuentra dentro de la caja (existe la pequeña probabilidad de que haya salido). Es obvio que cuanto más grande sea la caja, menos localizado tendremos al electrón. Aunque si lo observamos va a estar en un punto localizado, hasta ese momento se comporta como si pudiera estar en un reino mucho más grande. Pero él, en si mismo, no crece. Si lo observamos sobre una placa fotográfica seguiremos viendo un punto exactamente igual que el resto.