El enamoramiento es un estado de enajenación mental transitorio con una base bioquímica. Sin embargo, la decisión de mantener una relación sentimental con alguien de quien te has enamorado debería ser una decisión mucho más racional. En general, la gente se embarca en este tipo de relaciones que implican un compromiso, muchas veces en forma de matrimonio, tras una sesuda consideración Y, sin embargo, las tasas de ruptura son increíblemente altas: existe, diríamos, un fracaso en la implementación del programa vital acordado.
Esta es la “paradoja del fracaso”: el hecho de que ambos miembros de la pareja han planeado una relación duradera y se comprometen a trabajar para ella y la existencia de unas altas tasas de ruptura. Rey aborda en el artículo una aproximación matemática al problema, centrándose no en el análisis típico de los fallos en la relación, sino tomando la pareja como una unidad y basando su dinámica sentimental en el deseo de ser felices juntos para siempre. Lo que propone es un modelo matemático basado en la teoría del control óptimo para una pareja homógama (los miembros de la pareja se considera que poseen rasgos socioeconómicos semejantes) que se plantea una relación a largo plazo.
La teoría del control óptimo, una extensión del cálculo de variaciones, es un método de optimización matemática para deducir políticas de control. Un control óptimo adopta la forma de un conjunto de ecuaciones diferenciales que definen los valores de las variables de control que minimizan un coste, lo que se llama una política de control.
Rey define como variables dos funciones dependientes del tiempo: x(t), que representa el estado de la relación en el tiempo t, la sensación de que “la cosa va bien”, y c(t) , que es el esfuerzo hecho para mantener la relación (ésta es la variable de control). En la definición de c(t) Rey asume algo importante, que es continua. Incluye cualquier acto diario que sirva para reforzar la relación (hacer preguntas, la escucha activa, hacer planes juntos, etc.).
Rey establece en su modelo un sistema de dos ecuaciones diferenciales: la segunda ley de la termodinámica de las relaciones sentimentales, que afirma que una relación sentimental se deteriorará a menos que se aporte “energía” al sistema,
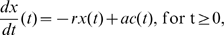
y la ley de variación del esfuerzo óptimo, que no es más que la expresión del esfuerzo óptimo en el tiempo t
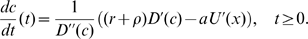
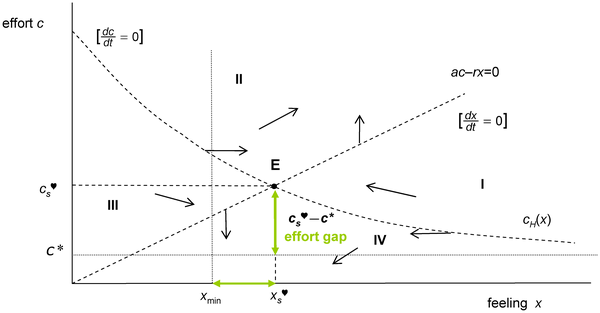
Con las premisas anteriores se alcanzan dos conclusiones matemáticas fundamentales. La primera es que existe un punto de equilibrio (equilibrio sentimental) sensación-esfuerzo (feeling-effort), E, y éste es único. La segunda, que existe una única política de esfuerzo (de la variable de control que hablábamos más arriba) que lleva la sensación inicial x0 al equilibrio único E.
5 comentarios:
Bueno, este es uno de esos estudios que te dejan entre divertido y meditabundo. Me gustaría hacer un comentario sobre las conclusiones del modelo y "El arte de amar" de Fromm, que me ha venido a la memoria mientras leía el post, aunque ya casi se me ha olvidado, la verdad.
Sea como sea, me encanta ver modelos matemáticos de cosas cotidianas, aunque este es posiblemente el más insólito con el que me he topado.
Me he acordado de esta entrada al ver esto
Hola, Rafa
Gracias por los comentarios.
El enlace que pones, muy bueno por cierto, es uno de los mejores ejemplos que conozco de las ventajas de saber matemáticas.
Un pedazo de resumen, al grano y con la rigurosidad del tratamiento matemático.
Como te digo en mi entrada, estoy tela de liado estos meses y sólo leo blogs una o dos veces a la semana. NO me gusta repetir información, si lo hubiera visto antes, no lo habría puesto.
Por supuesto, te he enlazado.
Saludetes.
No te preocupes, hombre, esto tampoco es el centro del universo. Me interesa mucho más que te haya gustado. Gracias.
Publicar un comentario