El momento angular orbital de la luz se puede determinar usando un orificio triangular.

La luz puede tener un “momento angular orbital”, un tipo de rotación que es más parecida a un planeta orbitando el Sol que a un planeta girando sobre sí mismo. Medir esta propiedad es complicado, pero un grupo de la Universidad Federal de Alagoas (Brasil) encabezado por Jandir Hickmann informa en Physical Review Letters de que un rayo de luz a través de un orificio triangular crea una patrón triangular de puntos que indica directamente el momento angular orbital de la luz incidente. Esta técnica sencilla añade otra herramienta para explorar esta propiedad inusual de la luz, que podría usarse algún día para codificar información cuántica.

Cuando un rayo de luz tiene momento angular puede haber dos contribuciones al mismo. El momento angular de spin, que corresponde a la polarización circular a derecha o izquierda de la luz, lo que implica que el campo eléctrico (recordemos que la luz es una radiación electro-magnética) rota en el sentido de las agujas del reloj o al contrario con respecto al sentido de avance del rayo. El momento angular orbital (que ha sido reconocido como algo real en los últimos 20 años) aparece si la dirección del campo eléctrico varía en el rayo. Por ejemplo, imagina que puedes ver el campo eléctrico de un rayo de luz con momento angular orbital que viene directo hacia tus ojos y que este rayo de luz tiene el diámetro de la esfera de un reloj. En una fase, es decir, en un tiempo dado, una aguja que indicase el campo eléctrico en la esfera del reloj puede dar una sola vuelta a la esfera (una unidad de momento angular orbital), dos (dos unidades), etc., de tal manera que cuando miramos el avance del rayo desde fuera, la aguja que representa el campo eléctrico va marcando la forma de un sacacorchos. El número de vueltas de la aguja, realmente del campo eléctrico, es lo que se llama “carga topológica”. Esta propiedad es la que se pretende poder controlar para que porte información, exactamente como se hace con la polarización.

Los experimentos de difracción generan patrones de puntos de luz y sombra que los físicos han venido usando para revelar las propiedades de la luz visible, pero las técnicas que existían para medir el momento angular orbital son pocas y más complicadas. Cuando Hickmann y sus colegas simularon la difracción de rayos que pasaban a través de orificios de varias formas, encontraron que el uso de un triángulo isósceles tenía una consecuencia inesperada: se pueden contar los puntos de luz para encontrar la carga topológica. Los investigadores verificaron esta predicción experimentalmente.

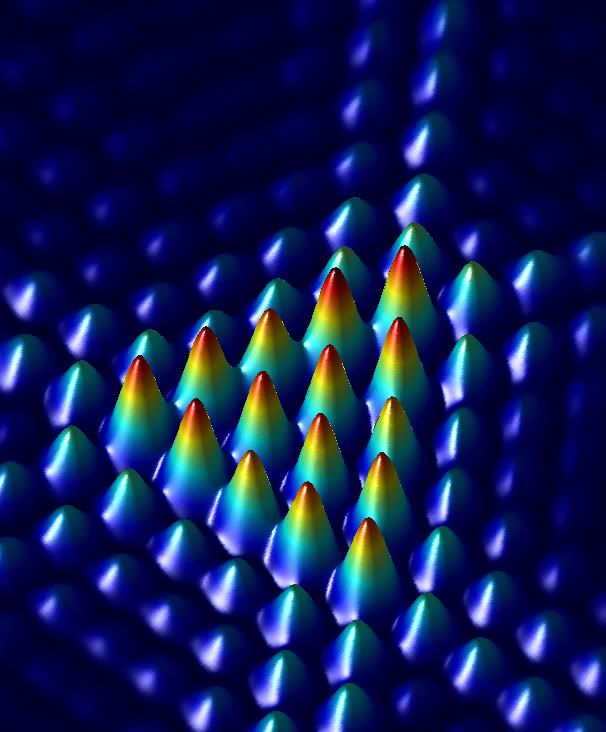
El equipo calculó primero y observó después que, una vez que el rayo está centrado en el agujero, genera un patrón inusual: una retícula triangular de puntos. El brillo de los puntos individuales depende de las contribuciones combinadas de la luz proveniente de las distintas localizaciones en el orificio triangular. Los cálculos predecían que los puntos más brillantes formarían un triángulo cuyo tamaño (el número de puntos en cada lado) sería el valor de la carga topológica más uno. Además este patrón triangular estaría girado 60 grados a un lado o a otro con respecto al orificio, dependiendo del signo de la carga (la dirección de la rotación de la luz). De esta manera una simple apertura triangular proporciona un método sencillo para medir tanto la magnitud como el signo del momento angular orbital.

Referencia:

Hickmann, J., Fonseca, E., Soares, W., & Chávez-Cerda, S. (2010). Unveiling a Truncated Optical Lattice Associated with a Triangular Aperture Using Light’s Orbital Angular Momentum Physical Review Letters, 105 (5) DOI: 10.1103/PhysRevLett.105.053904