Los isómeros del agua, ¿separados?

Hace casi nueve años Vladimir Tikhonov y Alesander Volkov de la Academia Rusa de Ciencias desataron una tormenta en medios científicos especializados cuando afirmaron que habían conseguido separar los dos isómeros de espín del agua. Ahora, T. Kravchuk et al., del Instituto de Tecnología Technion-Israel, afirman haber conseguido lo mismo pero usando una técnica diferente y sugieren que su resultado podría suponer un aumento espectacular en la calidad de los datos obtenidos en los experimentos no médicos con resonancia magnética nuclear (RMN). Publican su trabajo en Science.


Una molécula de agua puede ser uno de dos posibles isómeros de espín: en el “ortoagua” los espines de los núcleos átomos de hidrógeno están paralelos y en el “paraagua” los espines de los hidrógenos están antiparalelos. Los dos isómeros tienen propiedades fisicoquímicas sutilmente diferentes. Estas diferencias son importantes en diversos campos de la investigación. En astrofísica, por ejemplo, la proporción de orto y paraagua se utiliza para determinar las temperaturas en el espacio interestelar, aunque los datos son difíciles de interpretar, en parte porque no se han podido estudiar los isómeros por separado.


En 2002, Tikhonov y Volkov afirmaron haber creado gotas de agua enriquecidas en uno de los isómeros, estables durante al menos 25 minutos, basándose en las diferencias de adsorción en una superficie de los dos isómeros. Pero los experimentos no se pudieron reproducir de forma satisfactoria y hubo quien llegó a afirmar que sería imposible que las gotas se mantuviesen en un estado tan inestable durante tanto tiempo.


El grupo de Kravchuk podría haber encontrado la forma de superar los problemas del experimento de Tikhonov y Volkov empleando un método basado en las diferentes desviaciones que provoca la acción de un campo magnético en uno y otro isómero. El método implica hacer pasar un haz de vapor de agua a través de un imán de 6 polos que desviará cada molécula de agua en función de su espín. Kravchuk et al. habrían conseguido de esta manera un haz concentrado de vapor de ortoagua.


El trabajo de los investigadores ya ha despertado suspicacias, no tanto por el método, que habrá que reproducirlo experimentalmente (lo que parece posible), como por su afirmación de que la posibilidad de separar los dos isómeros permitiría aumentar la resolución de la RMN (no médica) hasta 100.000 veces. Esto sería real si el isómero aislado fuera estable pero, en cuanto el vapor de ortoagua sea capturado por un líquido o se deposite en una superficie, los espines de los hidrógenos cambiarían para producir una mezcla normal. 


Habrá que estar atentos a estos desarrollos: de confirmarse estaríamos ante una revolución en los métodos químico analíticos.

Referencia:


Kravchuk, T., Reznikov, M., Tichonov, P., Avidor, N., Meir, Y., Bekkerman, A., & Alexandrowicz, G. (2011). A Magnetically Focused Molecular Beam of Ortho-Water Science, 331 (6015), 319-321 DOI: 10.1126/science.1200433

El lado oscuro de los antioxidantes.

Durante años los medios de comunicación, las etiquetas de los alimentos y bebidas, los dietistas e incluso científicos que no están a la altura de su oficio nos han bombardeado con consejos para que consumamos suplementos de antioxidantes. Estas moléculas se encuentran de forma natural (aunque no sólo) en las frutas y verduras. Eliminan los radicales libres que, a su vez, son fracciones muy reactivas de moléculas que han sido señaladas como las responsables últimas del envejecimiento y de todo un abanico de enfermedades, desde el cáncer a las enfermedades coronarias.  Por decirlo de forma contundente, el que les haga caso y consuma suplementos de antioxidantes está poco menos que suicidándose, si entendemos por suicidio cualquier acción realizada por una persona que acorte significativamente su vida. ¿Exagero? Comprobemos los datos.

En los últimos años se habían venido acumulando pruebas de que tomar suplementos de antioxidantes, incluso algunos tan aparentemente inocuos  y comunes como las vitaminas C y E o el beta-caroteno, no es que no fuese beneficioso para la salud, sino que incluso podía ser perjudicial, aunque la causa tras la frase “parece incrementar la mortalidad” no estaba clara ( véase Antioxidantes: peor que inútiles ).

Pero, ¿por qué los antioxidantes pueden ser tan peligrosos cuando se ingieren como suplemento? Una hipótesis es que, a altas dosis, los antioxidantes pasan a ser oxidantes creando los efectos sobre el ADN y las células en general que se supone que deberían evitar. Otra hipótesis, seguramente más probable, es que estaríamos ante la versión humana de lo que se está encontrando en los ratones de laboratorio, esto es, los antioxidantes interferirían en la acción de las células del sistema inmunitario que combaten el cáncer y la infección. Efectivamente, los enemigos, los pérfidos radicales libres, realizan funciones muy importantes en el organismo. La principal, luchar contra las toxinas (los leucocitos de la sangre segregan cantidades muy grandes de radicales libres para combatir las infecciones bacterianas) y luchar contra las células cancerosas.

Cuanto más avanza la investigación más dudas aparecen sobre los beneficios de los antioxidantes, y cada vez más concretas. Veamos unos ejemplos, sin ánimo de ser exhaustivos.

Shkolnik et al. [1] han llegado a la conclusión de que los antioxidantes podrían afectar a la fertilidad femenina. El estudio, publicado en los Proceedings of the National Academy of Sciences, recoge que cuando se aplican antioxidantes a los ovarios de los ratones hembras, los niveles de ovulación caen drásticamente: los folículos ováricos liberan muchos menos óvulos. Esto sugeriría que la ovulación podría necesitar a los radicales libres que los antioxidantes neutralizan. Experimentos posteriores confirmaron esta idea: se produce una especie reactiva de oxígeno (ERO, una clase de radicales libres) como respuesta a la hormona luteinizante (lutropina), la señal fisiológica de la ovulación. Esto sugiere que la lutropina da inicio a la ovulación a través de una especie intermedia, el ERO. Si los antioxidantes eliminan el ERO, no habría ovulación.

Hsieh et al. [2] estudiaron los efectos en ratas diabéticas de dos antioxidantes populares, la quercetina y el ácido ferúlico  y encontraron que agravaban, y posiblemente provocaran, cáncer de riñón. Los propios autores lo dicen en el artículo del Journal of Agricultural and Food Chemistry: “Ya es hora de reevaluar el efecto contrario a la génesis de tumores de los antioxidantes”.

Finalmente, Barajas et al. [3], trabajando también con ratones, encuentran que la proteína que de forma natural aumenta los niveles de antioxidante en la sangre podría estar, de hecho, favoreciendo la arterioesclerosis. El estudio, publicado en Arteriosclerosis, Thrombosis, and Vascular Biology, explicaría por qué la ingesta de suplementos de antioxidantes no parece favorecer la salud cardiovascular. La proteína Nrf2 aumenta realmente los antioxidantes, pero en el estudio también aumentó los niveles de colesterol en sangre, así como el contenido en colesterol del hígado: dos formas excelentes de desarrollar arterioesclerosis.

La próxima vez que veas u oigas publicidad sobre los “beneficios” de los antioxidantes, recuerda que no existen píldoras milagrosas inocuas y ahorra tu dinero.  Si quieres aumentar tus años de vida y su calidad, el mejor consejo sigue siendo que hagas algo de ejercicio, comas sano, bebas moderadamente y no fumes.

Referencias:

[1]

Shkolnik, K., Tadmor, A., Ben-Dor, S., Nevo, N., Galiani, D., & Dekel, N. (2011). Reactive oxygen species are indispensable in ovulation Proceedings of the National Academy of Sciences, 108 (4), 1462-1467 DOI: 10.1073/pnas.1017213108

[2]

Hsieh CL, Peng CC, Cheng YM, Lin LY, Ker YB, Chang CH, Chen KC, & Peng RY (2010). Quercetin and Ferulic Acid Aggravate Renal Carcinoma in Long-Term Diabetic Victims. Journal of agricultural and food chemistry PMID: 20669956

[3]

Barajas, B., Che, N., Yin, F., Rowshanrad, A., Orozco, L., Gong, K., Wang, X., Castellani, L., Reue, K., Lusis, A., & Araujo, J. (2010). NF-E2-Related Factor 2 Promotes Atherosclerosis by Effects on Plasma Lipoproteins and Cholesterol Transport That Overshadow Antioxidant Protection Arteriosclerosis, Thrombosis, and Vascular Biology, 31 (1), 58-66 DOI: 10.1161/ATVBAHA.110.210906

¿Una cuantificación de la belleza musical?

No hace mucho participé en un debate sobre enfermedad mental y creatividad artística. Una de las impresiones que saqué es que algunas personas consideran que la belleza es algo objetivo e independiente del cerebro humano, una idea a la que no es difícil encontrar sus orígenes en Platón, y que la creatividad es una especie de don divino, una capacidad superior para encontrar esas “realidades artísticas”. Sin embargo, cada vez hay más evidencias de que “lo bello” no sería más que una adecuación de las características del objeto al cerebro en general y al estado del cerebro de un individuo en particular.

Una investigación realizada por Nicholas Hudson, de la Organización de Investigación y Ciencia Australiana (CSIRO, por sus siglas en inglés), cuyos resultados se publican en BMC Research Notes viene a profundizar en esta idea. Hudson ha comprobado algo muy simple: cuanto más compresible es una pieza musical más bella se considera. Esta hipótesis supone, por así decirlo, una cuantificación de la belleza musical. Partiendo de la base de que el cerebro tiende a simplificar la complejidad de los datos que recibe, el autor establece un paralelismo con el funcionamiento de los formatos de compresión  musical “sin pérdida” a la hora de reducir los archivos de audio quitando los datos redundantes e identificando pautas.

Hace mucho tiempo que existe la teoría de que la mente subconsciente puede reconocer pautas existentes en conjuntos complejos de datos y que nuestro cerebro habría evolucionado para encontrar las pautas sencillas como placenteras. Como decíamos antes, Hudson ha usado los programas de compresión musical “sin pérdidas” para imitar la capacidad del cerebro para condensar la información de audio. Ha comparado la capacidad de compresibilidad del ruido aleatorio con la de distintos estilos de música (clásica, pop, rock, tecno), encontrando que mientras que el ruido sólo puede reducirse a un 86% de su tamaño original, el pop, el rock y el tecno eran compresibles hasta alrededor del 60%, pero obras maestras aparentemente complejas como la Tercera Sinfonía de Beethoven podía ser comprimida hasta el 40%.

Hudson concluye que el máximo placer se extraería de composiciones musicales complejas para el oído pero que pueden ser descompuestas en pautas sencillas por el cerebro. Hasta aquí el estudio.

Asumiendo que esta correlación es, efectivamente causal, nos aventuramos a conjeturar que estos resultados serían un indicio de que nuestra apreciación por la música dependería de dos factores: la posibilidad de una composición para ser comprimida y de nuestra capacidad para poder comprimirla. Porque no todos los programas son iguales, podría ocurrir que hubiese composiciones que se pudiesen comprimir fácilmente al 60% y, otras, compresibles al 40%, a cuyo máximo sólo algunos podrían llegar. En esta línea, la escucha repetida de una obra permitiría un aprendizaje que facilitaría acercarse al máximo de compresibilidad para la misma; por tanto, aquellas obras cuyas escuchas repetidas permiten seguir comprimiéndolas serían las composiciones llamadas a convertirse en “clásicos”. Pero esto, como siempre, son nuevas preguntas en busca de una respuesta.  

Referencia:

Hudson NJ (2011). Musical beauty and information compression: complex to the ear but simple to the mind? BMC research notes, 4 (1) PMID: 21251325

BZ: un oscilador espaciotemporal químico.

Cuando Boris P. Belousov, a la sazón director del Instituto de Biofísica de la Unión Soviética, envió un artículo en 1951 a un prestigioso journal científico en el que afirmaba que había encontrado una reacción química oscilante, se encontró con un rechazo rotundo. De hecho recibió una nota del editor, un prestigioso bioquímico, en la que, tajantemente, afirmaba que eso era, simple y llanamente, “imposible”. Y eso a pesar de que el procedimiento para llevar a cabo la reacción no podía ser más sencillo para un laboratorio como el de este editor, pero su convicción de que eso no podía ser era tan profunda que ni se tomó la molestia de comprobarlo experimentalmente.

En muchos campos de la ciencia existen fenómenos periódicos, sistemas que oscilan siguiendo pautas. Imaginemos, por ejemplo, un péndulo (física), los ritmos circadianos (biología) o las funciones sinusoidales (matemáticas). Pero, ¿es posible un sistema químico oscilante? Tras un poco de reflexión es probable que se llegue a la conclusión de que no es posible su existencia porque se estaría violando la Segunda Ley de la Termodinámica, así, con mayúsculas. Muchos grandes químicos, incluido el editor que rechazó el artículo de Belousov, han sido de esta opinión. El problema de este enfoque es que es erróneo de raíz. A todos los que hemos estudiado algo de física o matemáticas nos han hecho siempre mucho hincapié en la importancia de saber para qué condiciones de contorno está desarrollada una determinada fórmula y que, aplicarla fuera de esas condiciones, no tiene sentido matemático/físico. Al afirmar que una reacción química oscilante no es posible estamos incurriendo exactamente en este error: aplicamos los conceptos de la termodinámica del equilibrio (desarrollada por Gibbs a finales del siglo XIX y prácticamente la única que se estudia durante los estudios de grado/licenciatura) a todos los sistemas, pero olvidamos que existen sistemas que están lejos del equilibrio para los que no tiene sentido físico su uso.

Belousov había estado intentando crear un modelo del ciclo de Krebs cuando, completamente por accidente, observó que una disolución de ácido cítrico, bromato (BrO₃^-) y una sal de cerio (Ce) oscilaba periódicamente entre amarillo e incoloro. Sin embargo, debido a la resistencia entre la comunidad química a aceptar la mera posibilidad teórica de los osciladores químicos, el trabajo no se pudo publicar [1] hasta años después y sólo en los resúmenes de una oscura conferencia médica. Aquel “incidente” acabó con la carrera de Belousov.

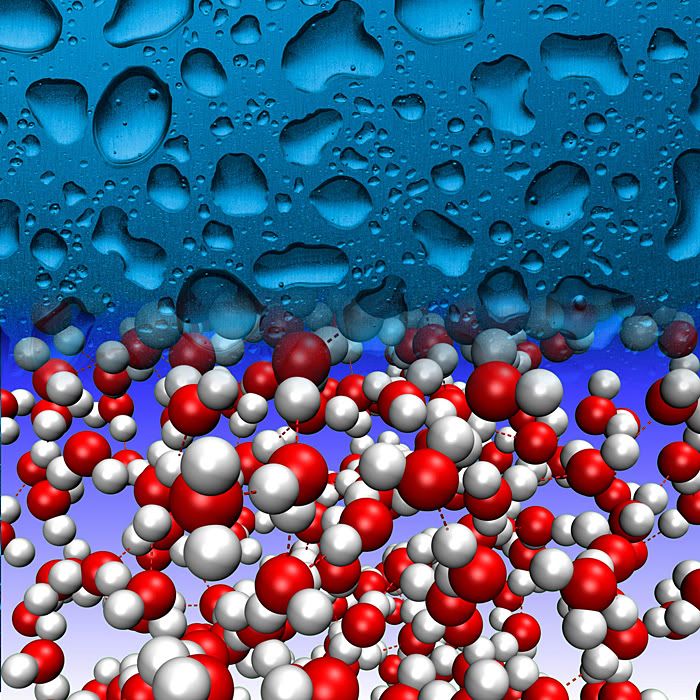
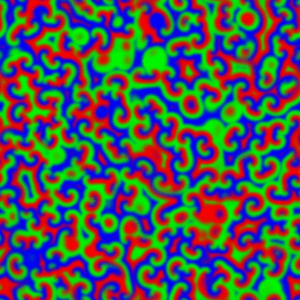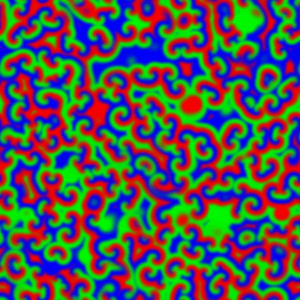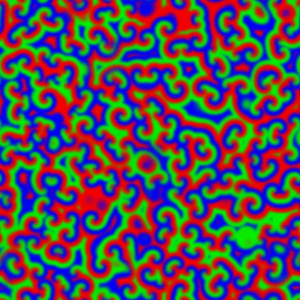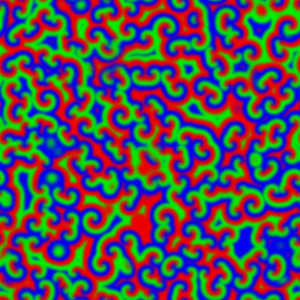
Afortunadamente el testigo fue recogido años después por otro biofísico, Anatol M. Zhabotinsky, actualmente en la Universidad Brandeis (EE.UU.). Zhabotinsky refinó la reacción, reemplazando el ácido cítrico por malónico y descubriendo que cuando una fina capa homogénea de los reactivos se deja evolucionar sin intervención posterior, aparecen fascinantes patrones geométricos [imagen izquierda] como círculos concéntricos y espirales de Arquímedes que se propagan por el medio (véase vídeo 1, vídeo 2). Por lo tanto, la reacción oscila tanto en el tiempo como en el espacio, por lo que es un oscilador espaciotemporal. Zhabotinsky también se encontró con la resistencia de los editores que usaban el argumento de la imposibilidad termodinámica, pero un conocimiento más extendido de la termodinámica del no-equilibrio permitió que Zhabotinsky consiguiese publicar [2] finalmente varios artículos sobre la que hoy se conoce como reacción de Belousov-Zhabotinsky o, simplemente, reacción BZ. Las pruebas estaban ahí: las reacciones químicas podían oscilar, y hacerlo periódicamente.

Pero la reacción BZ se quedaría en una mera curiosidad si no se pudiese describir completamente lo que ocurre en realidad. Y una descripción no es completa si su dinámica no puede expresarse en el lenguaje de la ciencia: las matemáticas. A principios de los años 70 del siglo pasado Richard Noyes, Richard Field y Endre Koros, los tres en la Universidad de Oregón (EE.UU.), propusieron [3] un mecanismo consistente en 18 reacciones químicas y 21 especies químicas diferentes o, lo que es lo mismo, un espectacular e intimidante sistema de ecuaciones diferenciales para describir las velocidades de las distintas reacciones. El sistema es tan difícil de aprehender que los autores crearon una simplificación del mecanismo, llamada “Oregonator”, para poder explicarlo. A pesar de su relativa simplicidad, el Oregonator es capaz de capturar el comportamiento “cualitativo” de la reacción BZ.

El Oregonator reduce las reacciones de 18 a 5. Aparecen a continuación junto a las velocidades de reacción asociadas (v):

BrO₃^- + Br^-- ->  HBrO₂ + HOBr //  v₁ = k₁[BrO₃^-][Br^-]

HBrO₂ + Br^-- ->  2HOBr // v₂ = k₂[HBrO₂][Br^-]

BrO₃^- + HBrO₂ ->  2HBrO₂ + 2Ce⁴⁺ // v₃ = k₃[BrO₃^-][HBrO₂]

2HBrO₂ ->  BrO₃^- + HOBr //  v₄ = k₄[HBrO₂]²

B + Ce⁴⁺  -> 1/2fBr^- // v₅ = k_c[B][Ce⁴⁺]

Donde B representa todas las especies orgánicas oxidables presentes y f es un factor estequiométrico que recoge la química orgánica presente. Recordemos que en la notación de las velocidades de reacción las especies entre corchetes representan la concentración (en una unidad apropiada, habitualmente moles por litro) de dicha especie. Las k_i son simplemente constantes de reacción que dependen de la temperatura y deben determinarse experimentalmente.

Con objeto de facilitar la lectura vamos a llamar A a la concentración de BrO₃^-, B a la de todas las especies orgánicas oxidables, P a la del HOBr, X a la del HBrO₂, Y a la del Br^- y Z a la del Ce⁴⁺. Si todavía hacemos una simplificación más y tratamos a las concentraciones A y B como constantes, entonces las velocidades de reacción de X ,Y ,Z, que describen el comportamiento de este sistema simplificado serían (P, es un producto y por tanto depende de X ,Y , Z, A y B):

dX/dt = k₁AY - k₂XY + k₃AX – 2k₄X²

dY/dt = - k₁AY – k₂XY + f/2·k_cBZ

dZ/dt = 2k₃AX – k_cBZ

Este sistema de ecuaciones diferenciales se resiste a ser resuelto analíticamente pero se puede abordar por métodos numéricos. Cuando A = 0,06M, B=0,02M y f =1, se puede observar efectivamente un comportamiento oscilatorio:

La descripción del mecanismo y de la dinámica de la reacción BZ ha posibilitado su uso como modelo para el estudio de otros sistemas complejos como el crecimiento bacteriano [imagen derecha, D. discoideum] o el estudio de ciertas propiedades de las neuronas. También basándose en la reacción BZ se pueden crear puertas lógicas “húmedas”.

Referencias:

[1]

Belousov B. P., A periodic reaction and its mechanism,in Collection of short papers on radiation medicine for 1958, Med. Publ., Moscow, 1959.

[2]

Zhabotinsky, A. M., Periodical oxidation of malonic acid in solution (a study of the Belousov reaction kinetics), Biofizika, 9, 306-11 (1964).

[3]

Field, R. J., Koros E., and Noyes, R. M., Oscillations in chemical systems .2. Thorough analysis of temporal oscillation in bromate-cerium-malonic acid system, J. Amer. Chem. Soc. 94, 8649-64 (1972).

Esta entrada es la segunda participación de Experientia docet en el XV Carnaval de la Física que este mes organiza Curiosidades de la Microbiología.

Esta entrada es la tercera participación de Experientia docet en el I Carnaval de la Química que organiza Ese punto azul pálido.

Esta entrada es la segunda participación de Experientia docet en el X Carnaval de Matemáticas que organiza La Ciencia de la Mula Francis.

Hierro: química verde para el agua.

La presencia de hierro en el agua se considera contaminación. Sin embargo, está a punto de comercializarse una nueva tecnología que usa una forma exótica de hierro para limpiar el agua, incluido el propio hierro.

El hierro (Fe) es un metal de transición. Como todos los metales reacciona con otros elementos donando electrones y formando iones cargados positivamente (cationes). Los metales de transición, sin embargo, son capaces de donar diferente número de electrones dependiendo de las circunstancias y, por lo tanto, forman cationes de distintas cargas. Habitualmente, el Fe pierde dos (Fe²⁺) o tres (Fe³⁺) electrones. Pero en los ferratos, que son compuestos  de Fe y oxígeno (O) con metales alcalinos (como el sodio, Na) o alcalinotérreos (como el calcio, Ca) cede 6 electrones (en el caso que nos ocupa), formando [FeO₄]^2-, lo que lo hace tremendamente reactivo.

En primer lugar los ferratos son agentes oxidantes fuertes. Tanto que son capaces de destruir rápidamente bacterias, virus y moléculas orgánicas en general. En segundo lugar, los ferratos son excelentes coagulantes y floculantes: atraen a otros compuestos presentes en el agua, incluidos los metales disueltos, y los precipitan. Además, cuando han terminado su trabajo, el Fe del ferrato precipita como óxido férrico (Fe₂O₃).

¿Y por qué no es universal ya el uso de esta panacea para purificar el agua? Imaginemos lo que sería disponer de este producto en lugares donde las aguas suelen estar contaminadas química y microbiológicamente. Pues por las mismas razones que lo hacen tan eficaz: su reactividad lo hace tan inestable que es muy difícil de almacenar.

Una compañía estadounidense, FTT , cree haber encontrado una solución que, si bien no es la ideal, sí puede ser operativa. En vez de fabricar y transportar el ferrato, lo fabrican allí donde se vaya a usar. FTT ha construido una miniplanta móvil que es capaz de sintetizar ferrato a partir de tres productos básicos: lejía (HOCl), cloruro férrico (FeCl₃) y sosa cáustica (NaOH). La reacción sería como sigue:

2Fe³⁺ + 3OCl^- + 10OH^- -> 2[FeO₄]^2- + 5H₂O + 3Cl^-

La planta de FTT, que es lo suficientemente pequeña como para ser transportada en un pick-up, tiene capacidad para producir ferrato suficiente para purificar 75 millones de litros de agua al día. En estos momentos hay dos plantas experimentales en funcionamiento, puede que a final de año lo esté la primera planta comercial.

Esta entrada es la segunda participación de Experientia docet en el I Carnaval de la Química, que organiza Ese punto azul pálido.

Cliodynamics: una aproximación matemática a la historia.

Hay personas para las que saberse dueñas absolutas de sus actos, resultado exclusivo de su voluntad libre, es tremendamente importante. Estas personas no suelen llevar bien que cada vez más aspectos de la toma de decisiones humana se revelen inconscientes o, en algunos casos, directamente irracionales, puramente instintivos. El comportamiento de una bandada de pájaros o un enjambre de insectos puede simularse a partir de unas condiciones muy sencillas para el comportamiento de cada individuo. Ahora empieza a consolidarse una nueva rama del conocimiento que busca leyes generales en la historia mediante métodos matemáticos. Se publica el primer número de Cliodynamics: Journal of Theoretical and Mathematical History.

Carl Hempel publicó en 1942 el ensayo “La función de las leyes generales en la historia” en el que argumentaba que la explicación histórica debía invocar leyes generales, como cualquier otra explicación científica. Este ensayo provocó un debate entre los filósofos de la historia en el que se pueden encontrar argumentaciones similares a las que se encuentran en los debates sobre la existencia del alma humana. Así, y a título de ejemplo, Daniel Little en su artículo  para la Stanford Encyclopedia of Philosophy sobre filosofía de la historia, publicado en 2007, expresa su postura con un símil muy gráfico: “La explicación de las acciones humanas y sus consecuencias no debería ser del mismo estilo que la explicación de por qué los radiadores revientan cuando la temperatura baja de cero grados centígrados”.

Estas posiciones nos recuerdan lo que Baruch Spinoza escribió en el prefacio al libro tercero de su “Ética demostrada al estilo geométrico”, publicada en 1677: “La mayor parte de los que han escrito  acerca de los afectos y la conducta humana, parecen tratar no de cosas naturales que siguen las leyes ordinarias de la naturaleza, sino de cosas que están fuera de ésta. Más aún: parece que conciben al hombre, dentro de la naturaleza, como un imperio dentro de otro imperio. Pues creen que el hombre perturba, más bien que sigue, el orden de la naturaleza que tiene una absoluta potencia sobre sus acciones y que sólo es determinado por sí mismo.”

Poco a poco se va abriendo paso la visión de que es posible estudiar la historia desde una aproximación puramente científica, en la que los modelos matemáticos deben contrastarse con los datos empíricos. En esta línea, ya avanzada por Peter Turchin, su principal impulsor, en un artículo  en Nature en 2008, nace Cliodynamics.

Sorprendentemente las matemáticas son capaces de expresar las leyes que rigen el universo. Incluyendo las de la historia humana.

Esta es la participación de Experientia docet en el X Carnaval de Matemáticas que en esta ocasión alberga La Ciencia de la Mula Francis.

La actividad de una región del cerebro predice lo bueno que serás en un videojuego.

Simplemente escaneando tu cerebro con resonancia magnética (MRI) un grupo de investigadores encabezados por Loan Vo, de la Universidad de Illinois, afirma ser capaz de predecir “con una precisión sin precedentes” tu capacidad para jugar bien a un videojuego estratégico, es decir, tu capacidad para aprender una tarea compleja. El estudio aparece en PLoS ONE.

Para el estudio los investigadores usaron métodos para la obtención de imágenes por resonancia magnética convencionales, pero de una forma diferente. En vez de analizar el antes y el después de la actividad cerebral mientras los participantes aprendían  a realizar una tarea compleja, los científicos estudiaron la actividad de fondo de los ganglios basales, un conjunto de estructuras cerebrales asociadas con el aprendizaje de procedimientos, la sensación de recompensa y los movimientos coordinados.

A los datos obtenidos a partir de MRI estándar el equipo aplicó un análisis de las pautas multivolúmen (también llamado multivóxel, donde vóxel es volumetric pixel). El análisis reveló diferencias en un cierto tipo de señal, llamada T2*, en los ganglios basales de los voluntarios. Estudiando estas diferencias, los investigadores fueron capaces de predecir la varianza (diferencias en el desempeño), hasta en un 68 por ciento de las ocasiones  para las 34 personas que iban a aprender a jugar.

Los psicometristas han intentado predecir, usando una amplia variedad de tests, las probabilidades de éxito de una persona en una determinada tarea. En los países anglosajones, principalmente Estados Unidos, es muy conocido que las universidades usan los resultados en tests como SAT, GRE o MCAT para evaluar a sus candidatos. Estas técnicas, así como otras basadas en las dimensiones de estructuras cerebrales específicas, han tenido cierto éxito a la hora de predecir el aprendizaje, pero, salvando el tamaño de la muestra, en ningún caso han llegado a este nivel en una tarea tan compleja.

Para el estudio se eligieron voluntarios que no tenían mucha experiencia con videojuegos. Antes de que tuviesen contacto con el juego sus cerebros fueron sometidos a MRI, tras lo cual tuvieron 20 horas para aprender a jugar a Space Fortress, un juego desarrollado por la Universidad de Illinois y diseñado para evaluar las capacidades cognitivas de los participantes (y del que ya hablamos cuando vimos que unos de los efectos de jugarlo es una mejora neta de la capacidad intelectual). Básicamente consiste en destruir una fortaleza mientras defiendes a tu nave espacial de muchas amenazas posibles.

El juego es bastante difícil. Plantea retos continuamente al jugador que tiene que cambiar continuamente su foco de atención para perseguir objetivos o evitar amenazas. Cuando se comienza a jugar no es infrecuente alcanzar puntuaciones de 2.000 puntos negativos. Tras 20 horas de juego los resultados mejoran bastante en general. Sin embargo, algunas personas mejoran mucho más que otras y quién lo va  a hacer puede ser predicho a partir de la actividad de los ganglios basales antes de que conociese el juego. De hecho se predice tres veces la varianza (en aprendizaje) de lo que se haría usando otros métodos.

Dentro de los ganglios basales los investigadores se centraron en tres regiones: el núcleo caudado, el putamen y el núcleo accumbens. Las dos primeras son estructuras que se activan cuando una persona aprende nuevas habilidades motoras (hacer malabares o mover un joystick), cuando se realizan tareas que requieren estrategia o cuando se cambia rápidamente la atención. La tercera procesa las emociones relacionadas con la recompensa y el castigo.

Durante el estudio, la actividad en el putamen (en rosa en la  imagen) y en el núcleo caudado (en gris) resultó ser mejor predictora del desempeño futuro en el videojuego que la del núcleo accumbens. También encontraron que la cantidad de materia blanca (dendritas y axones de las neuronas, las conexiones) era mejor predictora que la materia gris (cuerpos celulares de las neuronas).

Parece conveniente en este punto recordar una cosa: el cerebro es plástico, por lo que una determinada configuración anatomofisiológica en un momento dado no es una condena al éxito o al fracaso a la hora de aprender o desempeñar una tarea; solamente puede ser un indicio de la cantidad de trabajo necesario.

Referencia:

Vo, L., Walther, D., Kramer, A., Erickson, K., Boot, W., Voss, M., Prakash, R., Lee, H., Fabiani, M., Gratton, G., Simons, D., Sutton, B., & Wang, M. (2011). Predicting Individuals' Learning Success from Patterns of Pre-Learning MRI Activity PLoS ONE, 6 (1) DOI: 10.1371/journal.pone.0016093

La postura corporal afecta a la autoestima.

Todavía me parece escucharla: “¡Tú recto! ¡La cabeza alta! ¡Mirando siempre a la punta de la Torre de La Equitativa*!”. Para mi abuela era muy importante la postura; según ella, influía mucho en cómo los otros te veían y en cómo te veías tú mismo. Ahora un estudio publicado en Psychological Science dirigido por Li Huang y Adam Galinsky, ambos de la Universidad Northwestern (EE.UU.), viene a confirmar esta idea.

Evidentemente la postura importa. El grande es el dominante en las distintas especies animales, incluida la humana, y las posturas que aumentan el tamaño aparente del individuo hacen que los otros le traten como si fuese más poderoso. No estaba tan claro que la postura afectase a la autoestima. Huang y Galinsky, para comprobarlo, compararon los efectos de la postura en la autoestima con los de un potenciador del ego mucho más convencional, las posiciones de mando. Sorprendentemente, concluyen que la postura puede influir incluso más.

En primer lugar los investigadores hicieron que 77 estudiantes voluntarios rellenasen unos cuestionarios, que parecían claramente diseñados para evaluar su capacidad de liderazgo. A la mitad de los sujetos se les dio un informe en el que se indicaba que, basándose en los cuestionarios, se le iba a asignar el papel de jefe en un experimento posterior. A la otra mitad se le dijo, también por escrito, que en dicho experimento serían subordinados. Mientras esperaban estos resultados se les pidió que participasen en un estudio de márketing para probar sillas ergonómicas. Esto implicaba que se sentasen en una silla de oficina en una postura específica al menos durante tres minutos. La mitad de los participantes se sentaban en posturas “contraídas”, con las manos por debajo de la cadera, las piernas juntas y los hombros hacia delante. La otra mitad en posturas “expansivas”, con las piernas separadas, la espalda recta y los brazos hacia fuera.

En realidad, ninguna de estas pruebas era lo que parecía. El cuestionario era irrelevante. A los voluntarios se les asignó un papel de jefe o de subordinado al azar. La prueba de la postura no tenía nada que ver con la ergonomía. De hecho, cada versión de postura tuvo el mismo número de futuros jefes que de subordinados. Una vez que terminó la prueba de la postura, los participantes recibieron su nuevo estatus como jefe o subordinado. Para evaluar la sensación de poder se pidió a los sujetos que realizaran una tarea de completar palabras. Esta tarea consistía en, dado un fragmento (“l_ad”, por ejemplo) completarlo para formar la primera palabra que viniese a la cabeza. Siete de los fragmentos podían interpretarse como palabras relacionados con el poder (las equivalentes en inglés para “poder”, “dirigir”, “liderar”, “autoridad”, “control”, “mandar” y “rico”). Cada uno de estos fragmentos que era interpretado como una palabra de poder (en nuestro ejemplo, “lead”, liderar, en vez de “load”, carga) significaba un punto para el participante, sin que éste lo supiese.

Aunque estudios anteriores sugerían que un simple cargo es suficiente para producir un incremento detectable en la sensación de poder de un individuo, Huang, Galinsky y sus colaboradores no encontraron diferencias en las puntuaciones de los voluntarios a los que se les dijo que eran jefes y las de aquellos a los que se les dijo que serían subordinados. La postura sí reveló diferencias. Los que se sentaron en una postura “expansiva”, independientemente de si pensaban que eran jefes o subordinados, obtuvieron un promedio de 3,44. Los que se habían sentado en posturas “contraídas” obtuvieron un 2,78.

Una vez establecido el principio, los investigadores compararon el efecto de la postura en decisiones relacionadas con el poder en distintas situaciones: hablar primero en un debate, tomar la iniciativa de abandonar el lugar de un accidente aéreo para buscar ayuda, o unirse a un movimiento para liberar a un prisionero encarcelado por error. En los tres casos aquellos que se sentaban en posturas expansivas elegían la acción activa (hablar primero, buscar ayuda, luchar por la justicia) más frecuentemente que los que habían tenido una postura “contraída”.

La conclusión, por tanto, es que mi abuela tenía razón. Los que andamos por ahí con la cabeza alta no sólo obtenemos el respeto de otros, también parece que nos respetamos más a nosotros mismos.

Referencia:

Huang L, Galinsky AD, Gruenfeld DH, & Guillory LE (2011). Powerful postures versus powerful roles: which is the proximate correlate of thought and behavior? Psychological science : a journal of the American Psychological Society / APS, 22 (1), 95-102 PMID: 21149853

* La Torre de La Equitativa es un edificio de Málaga.

Los coches arrancan por la relatividad de Einstein.

Los coches arrancan gracias a la teoría de la relatividad de Einstein. Esa es la conclusión a la que llega el equipo que encabeza Rajeev Ahuja, de la Universidad de Uppsala (Suecia), que, tras analizar cómo afectan al voltaje de las baterías plomo-ácido los efectos relativistas en las energías electrónicas de los átomos de plomo, calcula que dichos efectos suponen entre el 80 y el 85% de los 2,1 V que proporciona una celda de esas baterías. Los resultados aparecen en Physical Review Letters.

Desarrollada a mediados del siglo XIX, la célula de plomo-ácido es pesada y nociva, pero dado su bajo coste y potencia relativamente alta es la batería más común en los vehículos. Durante la descarga, el cátodo de plomo (Pb) y el ánodo de óxido de plomo (IV) (PbO₂), sumergidos en ácido sulfúrico (H₂SO₄), se convierten en sulfato de plomo (II) (PbSO₄).

En los átomos pesados la gran carga positiva del enorme núcleo es capaz de proporcionar tal energía a los electrones que éstos se mueven a velocidades significativamente próximas a la velocidad de la luz. La teoría de la relatividad predice entonces que su masa aumentará, alterando su distribución y la forma en la que los electrones interiores apantallan a los exteriores de la carga nuclear. El resultado es un desplazamiento en los niveles de energía electrónica y un cambio en los comportamientos químico y físico. El color amarillo del oro y el que el mercurio sea líquido a temperatura ambiente se debe a efectos relativistas, y se sabe desde hace mucho tiempo que estos efectos están presentes también en el plomo.

Ahuja y sus colaboradores han realizado cálculos químico cuánticos para determinar cómo la relatividad altera las estructuras de banda electrónica  del óxido de plomo y del sulfato. Encontraron que las capas s y p del plomo (especialmente la 6s) se estabilizan por efectos relativistas, especialmente en el óxido. Los investigadores calculan que la fuerza electromotriz de la célula de plomo-ácido es de 2,13 V, muy cerca del valor experimental. Los autores afirman que sin efectos relativistas el valor sería entre 1,7 y 1,8 voltios menor.

Este resultado implica que en el diseño de las baterías del futuro, si se emplean metales pesados, habrá que tener muy en cuenta los efectos relativistas en los cálculos teóricos preliminares. Si no se hace así se podrían descartar sistemas perfectamente viables.

Referencia: 

Ahuja, R., Blomqvist, A., Larsson, P., Pyykkö, P., & Zaleski-Ejgierd, P. (2011). Relativity and the Lead-Acid Battery Physical Review Letters, 106 (1) DOI: 10.1103/PhysRevLett.106.018301

Esta es la participación de Experientia docet en la XV Edición del Carnaval de la Física que, en esta ocasión, organiza Curiosidades de la Microbiología.

Químicos Modernos: El árduo camino al Nobel de Marie Curie.

El 10 de diciembre de 1911, Marie Curie recibía el premio Nobel de química por “los servicios para el desarrollo de la química  mediante el descubrimiento de los elementos radio y polonio”. Fue la primera mujer en recibir un premio Nobel y la primera persona en recibir dos (ella, Pierre Curie y Henri Becquerel habían compartido el premio de física de 1903 por su trabajo sobre la radiación). El impacto de Marie en el mundo científico, y en el papel de las mujeres en él, fue de tal magnitud que uno de los cuatro objetivos del Año Internacional de la Química 2011 (IYC2011) es celebrar el centenario de su premio. Con esta entrada Experientia docet le rinde homenaje e inaugura la serie Químicos Modernos que con motivo del IYC2011 dedica a los grandes personajes, muchos desconocidos, de la química del último siglo y medio.

Maria Salomea Sklodowska nació el 7 de noviembre de 1867 en Varsovia (Polonia). Sus padres eran ambos maestros (su madre murió cuando ella tenía 10 años) que supieron educar y motivar excepcionalmente a su hija. En aquella época Polonia era un estado súbdito de Rusia y las mujeres no tenían acceso a la educación superior, por lo que en 1891 Maria decidió unirse a su hermana Bronia en París, matriculándose en la Universidad de la Sorbona. Marie, ya con su nombre afrancesado, recibió sus títulos en física en 1893 y matemáticas en 1894 con calificaciones extraordinarias. La historia de cómo Marie llegó a titularse con 27 años en un país que no era el suyo, en un idioma que no era el suyo y teniendo que trabajar para sobrevivir nos habla ya de la extraordinaria mujer que era.

Conoció a Pierre Curie en la primavera de 1894, y se casaron en 1895 en una ceremonia civil en Sceaux (cerca de París). Ambos eran muy tímidos y nada mundanos, no preocupándoles gran cosa las ambiciones  económicas y sociales. Su principal afición era el ciclismo, pero ambos compartían también un profundo amor por la ciencia y una dedicación obsesiva a ella. Su primera hija, Irène, nacería en 1897.

Los resultados que obtuvo Pierre sobre la piezoelectricidad, la simetría de cristales y el magnetismo mientras era profesor en la Escuela Superior de Física y Química Industriales (ESPCI, por sus siglas en francés) de la ciudad de París siguen teniendo hoy día una importancia fundamental, especialmente los conceptos de temperatura de Curie (por encima de la cual los imanes pierden su magnetismo) y la ley de Curie que relaciona magnetismo y temperatura. Marie publicó su primer artículo en 1897 sobre la magnetización de los aceros pero buscaba un tema de investigación propio, que encontraría en la radioactividad. Un año después de la observación por parte de Wilhelm Röntgen de los rayos X en 1895, Henri Becquerel descubrió la radioactividad del uranio al comprobar cómo unas placas fotográficas envueltas en papel negro y guardadas cerca de unas sales de uranio se habían velado sin que les llegase luz.

A Marie se le concedió una habitación húmeda de la ESPCI para su investigación de doctorado. Allí pudo analizar toda una variedad de materiales inorgánicos, de entre los que el uranio y el torio eran los únicos elementos conocidos entonces que presentaban radioactividad. Sus muestras las colocó en una placa de condensador cargada hasta 100 V y unida a uno de los electrómetros de Pierre, pudiendo de esta forma medir cuantitativamente su radioactividad. Encontró que los minerales pechblenda (UO₂) y torbernita (Cu(UO₂)₂(PO₄)₂·12H₂O) eran más radioactivos que el uranio puro, de lo que dedujo que debían contener otros constituyentes aún más radioactivos. El 12 de abril de 1898 Marie presentó sus primeros resultados: “estos minerales podrían contener un elemento que sea mucho más activo que el uranio”. Pierre y ella decidieron que ella se concentraría en los aspectos químicos del aislamiento del elemento, mientras que el estudiaría sus “propiedades radiativas”.

En abril de 1898 Marie disolvió pechblenda en ácido clorhídrico (HCl) y trató la disolución con ácido sulfhídrico (H₂S): el uranio y el torio se mantenían en disolución, pero los sulfuros del precipitado seguían siendo muy radioactivos. Después de varias manipulaciones más encontró que este material radioactivo coprecipitaba con bismuto (Bi). En julio ella y Pierre publicaron un artículo (creando el nombre “radio-activo” en su título) presentado por Becquerel a la Academia de Ciencias. En él sugerían por primera vez que la radiactividad era un fenómeno asociado con el átomo y proponían que el nuevo elemento, una vez confirmada su existencia, debería llamarse polonio.

El análisis de las distintas fracciones del tratamiento de la pechblenda hizo que la pareja se diese cuenta de que debería haber otro elemento radioactivo, que no lo precipitaba ni el (H₂S), ni el sulfuro de amonio ((NH₄)₂S), ni el amoniaco (NH₃) y que formaba un carbonato insoluble en agua parecido al de bario BaCO₃ y un cloruro algo menos soluble que el de bario (BaCl₂) que actuaba de portador. A este elemento lo llamaron radio, publicando sus resultados el 26 de diciembre de 1898; el espectroscopista Eugène-Anatole Demarçay encontró una nueva línea espectral atómica del nuevo elemento, lo que ayudó a confirmar su existencia.

Dado que el nuevo elemento era mucho más radioactivo que el polonio, los Curie sus esfuerzos en él. Estaba claro que haría falta mucha más pechblenda para obtener cantidades significativas de radio. Terminarían procesando 8.000 kg de pechblenda austriaca. Durante los cuatro años siguientes trabajaron en unas condiciones y con unos medios que sólo pueden ser calificados como heroicos: en un cobertizo sin ventilación y sin calefacción, con un frío terrible en invierno y un calor abrasador en verano. Marie escribió: “Tuve que pasar todo el día mezclando una masa hirviente con una pesada barra de hierro casi tan grande como yo. Estaba rota de fatiga al acabar el día”. Sin embargo ella describió la vida en “este cobertizo miserable” como “los mejores y más felices años de nuestra vida”, y se sentía muy honrada cuando famosos científicos, entre ellos Lord Kelvin, de paso por París se acercaban a saludarles allí.

Trabajaron con lotes de 20 kg de pechblenda: moliendo, disolviendo y refinándola hasta conseguir pequeñas disoluciones. En 1902 consiguieron aislar 0,1 g de RaCl₂ después de miles de recristalizaciones a partir del más soluble BaCl₂ en HCl, determinando que el peso atómico del radio era 225. Marie completó su tesis doctoral, una de las más impresionantes que se recuerdan, en junio de 1903

En noviembre de 1903 los Curie y Becquerel recibían la noticia de que les había sido concedido el premio Nobel de física por su trabajo sobre la radioactividad. Becquerel acudió a Estocolmo, pero no así los Curie: Pierre estaba enfermo y desbordado con sus obligaciones y Marie se estaba recuperando de un aborto. El premio tuvo aspectos positivos y negativos: por una parte fue una ayuda financiera pero, por otro, les expuso a la alabanza y al escrutinio públicos. Marie escribiría más tarde “la pérdida de nuestro aislamiento voluntario fue causa de verdadero sufrimiento para nosotros”.

Se creó una cátedra para Pierre en la Sorbona con un puesto para Marie en 1904; en junio Pierre daba la conferencia Nobel en Estocolmo y al año siguiente Pierre fue elegido miembro de la Academia de Ciencias. En diciembre de 1905 nacía la segunda hija del matrimonio, Eve Denise. El lluvioso 16 de abril de 1906 Pierre resbalaba en el empedrado de la Rue Dauphine y moría en el acto al ser atropellado por un carro.

Marie pasó a ocupar la cátedra de la Sorbona de Pierre, convirtiéndose así en la primera catedrática de Francia. Ese mismo año Lord Kelvin escribió en el periódico The Times un artículo en el que especulaba con la posibilidad de que el radio podía ser un compuesto de plomo que contuviese cinco átomos de helio. Marie decidió probar más allá de toda duda razonable que el radio era un elemento. En 1907 consiguió 0,4 g de RaCl₂ y volvió a determinar el peso atómico, obteniendo 226,45. No satisfecha, en 1910 aisló el radio elemental por electrolisis de RaCl₂ en mercurio y destilándolo de la amalgama. Ya no había duda posible.

El 8 de noviembre de 1911 la Academia Sueca anunciaba que se había concedido el premio Nobel de Química  a Marie Curie por el descubrimiento del polonio y el radio.

Conferencia Amazing: El surgimiento de la química como ciencia exacta.

El próximo viernes 14 de enero a las 17:00, el que esto escribe dará una charla titulada “El surgimiento de la química como ciencia exacta” en el salón de actos de la Facultad de Matemáticas de la Universidad de Sevilla.

Esta charla se enmarca dentro del proyecto de innovación docente Divulgación Matemática para la Química, que los profesores de la asignatura Matemáticas del Grado en Química de la Universidad de Sevilla están llevando a cabo. Entre estos profesores está el amazing Tito eliatron (al que agradezco sobremanera la invitación).

La charla está abierta a todo el mundo y será muy divulgativa, sin una sola fórmula, ni matemática ni química. Los que tengan interés y no puedan asistir en persona, que sepan que Amazings.es puede que la emita en directo (esto deberá confirmarlo la propia web) y, en cualquier caso, será grabada y colgada en internet  (ya informaremos sobre dónde está disponible).

Si eres lector de este blog y te pasas por allí no dudes en acercarte a saludar, estaré encantado de conocerte.

4 segundos de significativo silencio.

Tan sólo cuatro (4) segundos de silencio durante una conversación son suficientes para evocar los miedos primarios, que activarán esas sensaciones tan angustiosas de incompatibilidad y exclusión. Esta es, al menos, una de las conclusiones a las que ha llegado el equipo de investigación encabezado por Namkje Koudenburg, de la Universidad de Groninga (Países Bajos), y que publica en el Journal of Experimental Social Psychology.

El que una conversación sea fluida se asocia con emociones positivas, favorece un sentimiento de pertenencia, de autoestima, de validación social y de consenso. Sin embargo, la interrupción de esa fluidez con un silencio breve produce sentimientos de rechazo y emociones negativas.

Para el estudio, los investigadores realizaron dos experimentos en los que analizaron la respuesta de los participantes a silencios incómodos. En el primero, 102 universitarios leyeron una de dos historias. La primera versión describía a alguien que hacía un comentario desconsiderado (“Creo que las personas obesas debería pagar por dos asientos en el autobús”) que iba seguido por un silencio. En la historia alternativa la conversación seguía como si nada tras el comentario. A los estudiantes se les pedía que se imaginasen en la situación de la persona que había hecho ese comentario. No es sorprendente que dijeran sentirse más ansiosos, rechazados y menos seguros en la situación con el silencio que en la alternativa.

En el segundo experimento 60 estudiantes visionaron vídeos de dos situaciones alternativos en los que el comentario inapropiado se hacía en una conversación sobre relaciones personales y se refería al sexo entre profesores y alumnos. En un caso, la afirmación era seguida por un silencio de cuatro segundos; en la otra versión  la conversación continuaba como si nada. Si bien los vídeos no contenían referencias al silencio y los sujetos ni siquiera fueron conscientes de la pausa, los estudiantes que vieron la versión que contenía la rotura de la conversación volvieron a valorar sus sentimientos de rechazo como mayores y su autoestima más baja.

La hipótesis es que la sensibilidad frente a los signos de rechazo y exclusión surgió durante la historia evolutiva de la especie, en la que hubo momentos en los que verse excluido de un grupo o la división de éste podía significar, literalmente, la diferencia entre la vida y la muerte. Estos días, afortunadamente, las consecuencias del rechazo social son bastante menos duras, aunque no siempre se sienta así.

Referencia:

Koudenburg, N., Postmes, T., & Gordijn, E. (2010). Disrupting the flow: How brief silences in group conversations affect social needs Journal of Experimental Social Psychology DOI: 10.1016/j.jesp.2010.12.006