En el siglo XIX físicos y químicos no tenían muy claro qué
podían ser los átomos y la imaginación se usaba para proveer
teorías que justificasen los datos experimentales. La consecución
de los espectros de los distintos elementos ponía de manifiesto que
existía una relación entre la radiación, la luz, y los átomos.
Como la luz se transmitía por el éter, ¿qué impedía considerar a
los átomos de los distintos elementos como perturbaciones en la
continuidad del éter? Ello justificaría de forma muy elegante esas
líneas oscuras y brillantes que aparecían en los distintos
espectros. Esta fue la idea que propuso en 1867 William Thomson, más
conocido como Lord Kelvin: los átomos no eran otra cosa que nudos en
el éter. La estabilidad topológica y la variedad de los nudos
serían un reflejo de la estabilidad de la materia y la variedad de
los elementos químicos. La teoría dio en llamarse teoría atómica
de los vórtices y estuvo en vigor hasta casi el siglo XX.
 |
| Espectros del neón (Ne), mercurio (Hg) y sodio (Na) |
 |
| Enlace de Hopf |
La idea de que los átomos eran nudos de vórtices de éter se le
ocurre a Thomson tras observar los experimentos que el
físico-matemático Peter Tait estaba realizando con anillos de humo
que, a su vez, se inspiraban en un artículo de Helmholtz sobre los
anillos vorticiales en fluidos incompresibles. Thomson y Tait
llegaron al convencimiento de que el estudio y la clasificación de
todos los nudos posibles explicaría por qué los átomos absorbían
y emitían luz en frecuencias determinadas. Thomson, por ejemplo,
creía que el sodio podría ser un enlace de Hopf debido a las dos
líneas características de su espectro. La teoría tenía el
respaldo de personajes de peso, como James Clerk Maxwell, que
afirmaba que la teoría satisfacía más condiciones que cualquiera
de sus competidoras.
Así pues, Tait se embarcó en solitario en la aventura de
realizar un estudio y tabulación completa de los nudos en un intento
de comprender cuando dos nudos eran “diferentes”. Sólo al final
recibió la ayuda de C.N. Litttle. La idea intuitiva de Tait sobre lo
que es “igual” y “diferente” es todavía útil. Dos nudos son
“isotópicos” (iguales) si uno puede ser manipulado de forma
continua en 3 dimensiones, sin que existan autointersecciones, hasta
que tenga el aspecto del otro.
 |
| Tabla (parcial) de nudos de Tait |
En la ilustración podemos ver parte del trabajo de Tait: una
enumeración de nudos y enlaces en términos del número de cruces en
una proyección plana. Si la teoría de Kelvin hubiese sido una base
correcta para la clasificación de los elementos químicos entonces
las tablas de nudos de Tait habrían sido los cimientos de la tabla
periódica. Pero la teoría de Kelvin demostró ser completamente
errónea, y físicos y químicos perdieron el interés por el trabajo
de Tait.
Una ley no escrita de la ciencia afirma que algunas veces los
problemas más interesantes se encuentran en la papelera de otro
investigador. Lo que los físicos abandonaron atrajo a los
matemáticos, que se centraron en la pregunta que se hizo Tait: ¿cómo
podemos dilucidar si dos nudos son isotópicamente iguales? La teoría
atómica fallida dejaba para iniciar el trabajo las 163 proyecciones
de nudos de Tait y una comprensión rudimentaria de la igualdad
isotópica en términos de manipulaciones de las proyecciones. Desde
el punto de vista matemático se había encontrado una mina de oro:
desde entonces la teoría de nudos ha ido creciendo sin parar, e
incluso a reentrado en la física teórica de la mano de la teoría
de cuerdas.
Pero la teoría se está reinventando a sí misma continuamente.
Sam Nelson, profesor del Claremont McKenna College (EE.UU.), publica
un artículo en Notices of the American Mathematical Society
en el que describe el nuevo enfoque en la teoría de nudos se ha ido
imponiendo en los últimos años y los objetos parecidos a nudos que
se han descubierto por el camino. Y ese enfoque parte de los
diagramas que representan a los nudos más que de los nudos mismos.
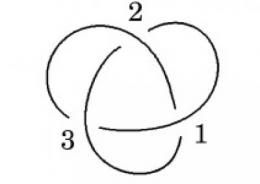 |
| E1D2E3D1E2D3 |
Desde el punto de vista matemático el cordón con el que se hace
el nudo es un objeto idealizado de una dimensión, mientras que el
nudo en sí es tridimensional. Los dibujos de los nudos, como los que
hizo Tait, son proyecciones del nudo en el plano bidimensional. En
estos dibujos se acostumbra a dibujar los cruces por encima o por
debajo del cordón como líneas continuas o discontinuas,
respectivamente (véase el diagrama). Si tres o más trozos del
cordón están uno encima de otro en un punto concreto, lo que se
hace es mover ligeramente los trozos sin cambiar el nudo de tal
manera que cada punto del plano tiene encima como mucho dos trozos.
Así, podemos decir que un diagrama plano de un nudo es la
representación de un nudo, dibujada en el plano bidimensional, en la
que cada punto del diagrama representa como mucho a dos puntos del
nudo. Los diagramas planos de nudos son una herramienta habitual en
matemáticas para representar y estudiar los nudos.
Pero, claro, manejar sólo diagramas no es posible, por lo que se
han desarrollados distintos métodos para representar la información
contenida en los diagramas de nudos. Un ejemplo es la notación de
Gauss, que no es más que una secuencia de letras y números en la
que a cada cruce en el nudo se le asigna un número y las letras E o
D, dependiendo de si el cruce se hace por encima o por debajo. Así,
en el nudo del diagrama vemos que si empezamos por 1 y seguimos hacia
la derecha el cordón pasa por encima (E1), da la vuelta para pasar
por debajo de 2 (D2), continúa para pasar por encima de 3 (E3),
luego por debajo de 1 (D1), encima de 2 (E2) y debajo de 3 (D3); por
tanto el código en notación de Gauss para ese nudo es E1D2E3D1E2D3.
A mediados de los años 90 del siglo XX los matemáticos
descubrieron algo extraño. Existen códigos de Gauss para los que es
imposible dibujar diagramas de nudos planos pero que, sin embargo, se
comportan como nudos en ciertos casos. En concreto, esos códigos,
que Nelson llama “códigos gaussianos no planos”, se comportan
perfectamente en algunas fórmulas que se emplean para investigar las
propiedades de los nudos.
Si un código gaussiano “plano” siempre describe un nudo en
tres dimensiones, ¿qué describiría un código gaussiano no plano?
Estaríamos hablando de sustancias etéreas de nuevo, nudos virtuales
que tienen códigos gaussianos válidos pero que no corresponden a
nudos en el espacio tridimensional. Estos nudos virtuales pueden
investigarse aplicando técnicas de análisis combinatorio a los
diagramas de nudos.
De la misma forma que, cuando los matemáticos se pararon a
considerar la posibilidad de que -1 tuviese una raíz cuadrada, se
descubrieron los números complejos (omnipresentes en física e
ingeniería), que encierran como “caso particular” los números
reales, ahora se ha descubierto que las ecuaciones que se usan para
investigar los nudos tridimensionales dan lugar a todo un universo de
“nudos generalizados” que tienen sus características
particulares pero que incluyen a los nudos tridimensionales como caso
particular.
¿Qué utilidad tendrá el descubrimiento más allá de las
matemáticas? No lo sabemos. En los libros de matemáticas están ya
las ecuaciones de la física del futuro. El problema de los físicos
es averiguar cuáles son.
Esta entrada es una participación de Experientia docet en la Edición 2.8 del Carnaval de matemáticas que alberga Cuanta Ciencia
Referencia:
Nelson, Sam "The Combinatorial Revolution in Knot Theory", Notices of the AMS December (2011) PDF

No hay comentarios:
Publicar un comentario