El origen matemático de los números cuánticos y de los orbitales atómicos.

En muchas ocasiones, cuando nos enfrentamos a la derivación de las expresiones matemáticas que representan sistemas físicos la mezcla precisamente de conceptos matemáticos y físicos hace que ni sigamos unos ni entendamos los otros. Nosotros pensamos que explicar ambas por separado ayuda en gran medida a la comprensión general.

Ayer, el hijo de un amigo nos planteaba que aceptaba la forma de los orbitales del átomo de hidrógeno y la aparición de los números cuánticos (salvo el de espín) como si fuesen un dogma, declarándose incapaz de seguir ni a su profesor ni a su libro de texto (el chaval estudia segundo de químicas en una prestigiosa universidad española). Es mi opinión que ello se debe a que las matemáticas y la física ya son lo suficientemente sutiles (me niego a aceptar que sean complicadas) por separado como, para encima, mezclarlas.

Lo que sigue es una explicación, un esquema conceptual si se quiere, de cómo se llega a los orbitales del átomo hidrogenoide (un átomo que tenga sólo un electrón) y a los 3 números cuánticos asociados (el de espín va aparte) desde un punto de vista matemático. Una vez que se tiene claro “cómo” lo haces ya te puedes concentrar en “qué” haces. Como conocimientos previos está saber lo que es una ecuación diferencial y cómo se resuelve en términos generales.

La llamada función de onda, que es la que describe la posición del electrón (por simplicidad excluimos la dependencia del tiempo), no es más que una función de tres variables que viene descrita por una ecuación diferencial llamada ecuación de Schrödinger (EdS) que adopta la forma

HΨ = EΨ                                [EdS]

donde H es un operador llamado hamiltoniano. Este operador a su vez lo podemos expresar de tal manera que la EdS la podemos escribir como

HΨ= aΔΨ + bΨ/r = EΨ           [EdS]

en la que a y b son constantes, Δ es el operador laplaciano y r es una distancia (la del electrón al núcleo). El operador laplaciano no es más que la suma de las derivadas parciales segundas con respecto a cada una de las tres variables, es decir:


a(∂²Ψ /∂x² + ∂²Ψ /∂y² + ∂²Ψ /∂z²) + bΨ/r = EΨ [EdS]

r = (x²+y²+z²)^1/2

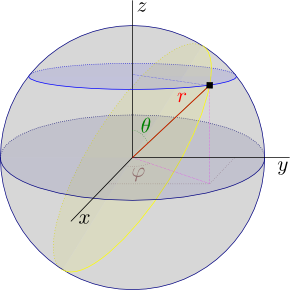Coordenadas esféricas físicas.

La resolución de esta ecuación diferencial nos proporcionará Ψ, que es lo que queremos. Sin embargo esta resolución en coordenadas cartesianas se hace muy complicada y es preferible usar coordenadas esféricas. En estas coordenadas Ψ pasa de ser una función de x, y, z a ser una función de r, θ y φ donde

x = r sen θ cos φ

y = r sen θ sen φ

z = r cos θ

Haciendo la sustitución resulta que la función Ψ puede expresarse como el producto de tres funciones cada una de una sola variable, Ψ= R(r)Θ(θ)Φ(φ), con lo cual obtenemos tres ecuaciones diferenciales independientes, cada una en una sola variable. Ya sólo nos queda resolver estas ecuaciones. No vamos a entrar aquí en cómo se hace, nos limitaremos a señalar unos detalles matemáticos que después se revelarán como muy importantes.

En la resolución de Φ(φ) nos va a aparecer una constante de separación que, convencionalmente (tiene un sentido físico), llamaremos m. Para que se cumpla que Φ(φ) = Φ(φ +2π), m sólo puede ser un número entero (positivo, negativo o cero).

La resolución de Θ(θ) es más complicada. En ella aparece de nuevo m y una nueva constante de separación l. Las condiciones que deben cumplir las soluciones (que sean cuadráticamente integrables) obligan a que l = |m|, |m|+1, |m|+2,.... Esto quiere decir que el valor más pequeño de l es cero y que m va de -l a +l de 1 en 1.

Finalmente, en la resolución de R(r) aparece de nuevo l y otra constante de separación n que, por un razonamiento análogo al anterior resulta que debe ser mayor o igual a l+1. Deducimos de aquí que el valor más pequeño de n es 1.

Es necesario recordar que estas soluciones no son funciones únicas sino familias de funciones que cumplen los condicionantes de la EdS y que los distintos miembros de las familias vienen dados por los distintos valores permitidos de n, l y m. Y esto es matemáticas, no física.

Bien, pues ya tenemos encontradas las soluciones a la EdS, que tienen la forma general

Ψ = R_nl(r)Θ_lm(θ)Φ_m(φ)

donde, como hemos visto,

n = 1,2,3,...

l = 0,1,2,...,n-1

m = -l, -l+1,...,0,...,l-1,l

Veamos el aspecto de algunas de estas soluciones. Si hacemos n =1, ello implica que l = 0 y m = 0. En este caso Θ(θ) y Φ(φ) se hacen constantes y

Ψ =Ψ(r) = Ae^Br (A,B son constantes de integración)

Para n = 2 tenemos esta misma posibilidad ( l = 0 y m = 0) y tres más a partir de l=1 con m = +1,0,-1, a saber,

Ψ = Ce^Br

Ψ = D r sen θ cos φ e^Br

Ψ = D r sen θ sen φ e^Br

Ψ = D r cos θ e^Br (C, D son constantes de integración)

Y así podríamos seguir para los distintos valores de n, l y m encontrando todos los miembros de la familia de funciones que son solución de la EdS.

Aproximémonos ahora un poco a la terminología física. La representación de las funciones que sólo dependen de r será una esfera, llamemoslas s y distingámolas por el valor de n:

1s = Ae^Br

2s = Ce^Br

Las funciones que tengan l =1, llamémoslas p, distingámolas por su valor de n y marquemos con un subíndice su orientación en ejes cartesianos (transformamos ahora de esféricas a cartesianas):

2p_x = D r sen θ cos φ e^Br = D x e^Br

2p_y = D r sen θ sen φ e^Br = D y e^Br

2p_z = D r cos θ e^Br = D z e^Br

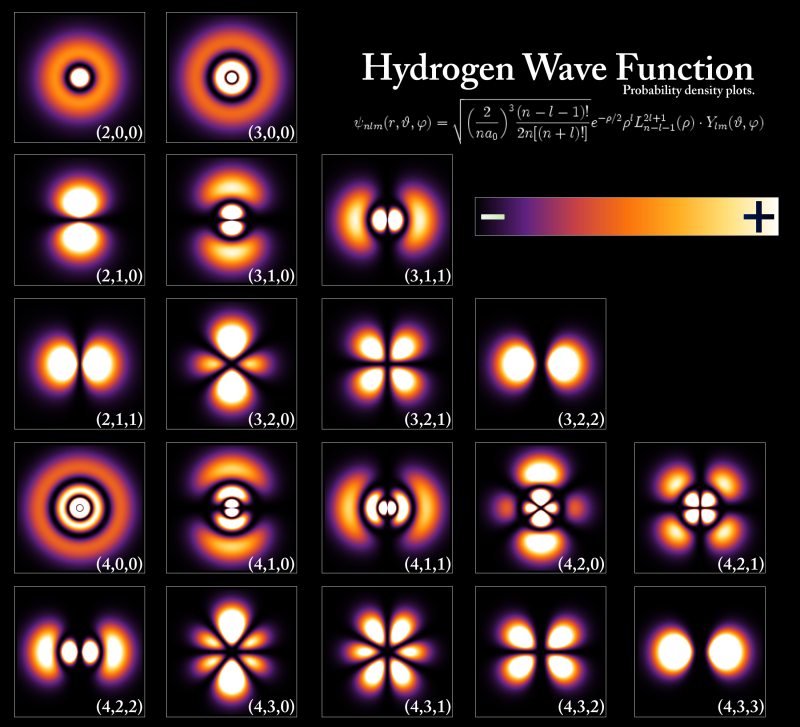
Tenemos de esta forma las funciones de onda reales hidrogenoides para n =1 y n = 2. Un orbital es una función de onda espacial de un electrón. Puesto que en un átomo hidrogenoide solo tiene un electrón, todas sus funciones de onda son orbitales. Éstos tienen la siguiente representación gráfica:

Finalmente damos nombre a nuestras constantes de separación, que llamaremos números cuánticos porque, como hemos visto, adoptan valores discretos (no continuos):

n es el número cuántico principal

l es el númnero cuántico de momento angular y

m es el número cuántico magnético.

Ya podemos comprender la imagen del comienzo de la entrada sabiendo que los números entre paréntesis corresponden a los tres números cuánticos. Y ya está. Lo demás son detalles.