En estos días ha habido mucho revuelo mediático con la
posibilidad de que los neandertales hubiesen tenido la oportunidad de
ser los pintores de Altamira y otras 10 cuevas del norte de España
(véase este enlace como ejemploy más datos) . A lo que no se ha prestado atención alguna es al
método empleado, que en el artículo publicado en Science,
Pike et al. llaman “datación por serie U”. Vamos a
explorar la base teórica (incluidas las matemáticas) del mismo, que
es muchísimo más sencilla que la experimental, porque si bien no
hay nada más práctico que una buena teoría, también es cierto que
aún no debiendo haber teóricamente diferencia entre teoría y
práctica, en la práctica, la hay.
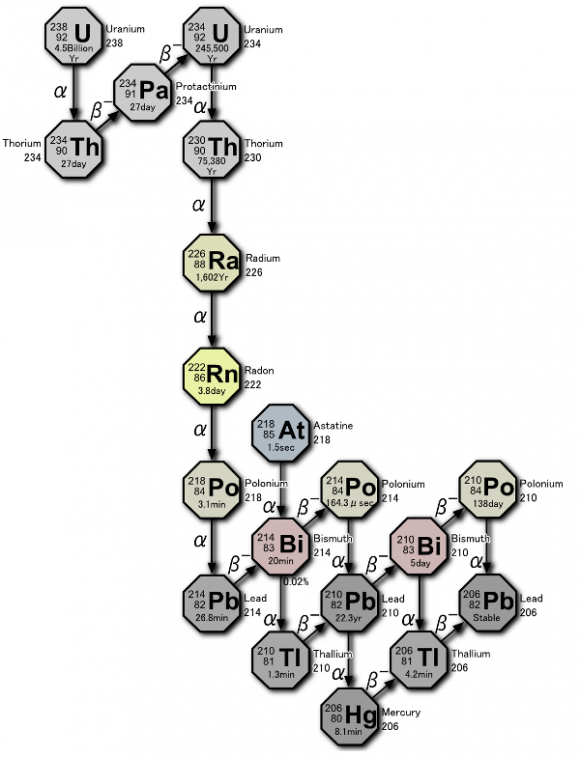
Los investigadores usaron los ratios entre los isótopos
uranio-234 y torio-230 para datar los depósitos de calcita
sobrepuestos a las pinturas para calcular la edad mínima de las
mismas. Los resultados, con edades mínimas en el entorno de los
40.000 años de antigüedad, abren distintas posibilidades. Como se
supone que Homo sapiens sapiens no migró a Europa hasta hace poco
más de 40.000 años es probable que trajese sus habilidades
artísticas africanas con él y decorase las cuevas poco después de
llegar o, quizás, las pinturas más sencillas y antiguas fuesen de
hecho la obra de neandertales.
La datación uranio-torio es especialmente interesante en el
análisis de carbonatos cálcicos, como la calcita, ya que ninguno de
los elementos puede escapar del mineral, ni otros átomos de ellos
pueden entrar, una vez se ha formado. En las condiciones de formación
de las calcitas el uranio es soluble mientras que el torio no lo es,
por lo que cuando se forma el depósito mineral contendrá uranio
pero no torio. La cantidad del isótopo U-234, que es el isótopo que
por desintegración alfa se convierte en torio 230, que podemos
esperar tener en una calcita recién formada es del orden de partes
por millón o inferiores. Suponiendo que sepamos la cantidad original
de uranio presente en la muestra, necesitamos poder calcular cuánto
Th-230 tendremos pasado un tiempo a partir de una determinada
cantidad de U-234 para tener un método para determinar el tiempo
transcurrido.
-dN/dt = λN
Esto es una ecuación
diferencial muy sencillita que el lector puede comprobar que tiene
como solución
N = N0 e-λt
, donde N0
es el número de átomos pata t
= 0. [1]
Sin
embargo, el sistema U-234 - Th-230 no es tan sencillo, puesto que el
Th-230 también se desintegra. Estamos entonces ante esta situación:
A →
B →
C. El razonamiento es análogo: si tengo N
núcleos, pasado un tiempo infinitesimal dt,
tendré N+dN
núcleos. En este caso escribo +dN,
porque dN
puede ser positivo o negativo, dependiendo de si se forman más
núcleos de los que se desintegran o al revés. En cualquier caso, la
variación en el número de núcleos será los que se forman menos lo
que se desintegran, por tanto, usando [1]:
dNB/dt
= λANA
– λBNB
= λA N0A
e -λAt
– λBNB
Esto sigue siendo una ecuación
diferencial nada complicada, que se puede comprobar que tiene como
solución:
NB = (NA0
λA)
/ (λB
- λA)
· (e -λAt
- e -λBt) [2]
En pura teoría ya tenemos la ecuación
que buscábamos. Si conocemos las constantes de los isótopos U-234
(que ocupa el lugar de A) y del Th-230 (B), que las
conocemos, tendríamos un método para medir la antigüedad de los
depósitos de calcita.
El inteligente lector que haya llegado
hasta aquí se habrá dado cuenta de que venimos arrastrando un
problema no menor desde el principio: ¿cómo sabemos qué cantidad
había al comienzo del isótopo A, lo
que hemos llamado NA0?
Simplemente, no lo sabemos, ni lo podemos saber con suficiente
precisión. Por eso un método de datación que se base en una serie
radioactiva sólo es válido si uno de los núcleos es estable (λB
= 0)
o, como el caso de U-234 y Th-230, que se cumpla que
0
< λA
<< λB
Entonces [2] queda reducida a
NB / NA
≈
λA
/ λB
(1 -
e -λBt) [3]
Ya que
también en este caso, NA
≈ NA0.
Vemos pues que si medimos por
espectrometría de masas el ratio Th-230/U-234 tenemos una forma
directa de medir el tiempo desde que se formó la calcita con un
error más que razonable. Sólo nos quedará corregir por la cantidad
de U-238 que se convierta en U-234, pero eso es más de lo mismo (se
deja al lector como ejercicio).
Observando la ecuación [3] vemos una
de las limitaciones del método: para tiempos suficientemente grandes
NB / NA tiende a un
valor constante λA
/ λB,
es lo que se denomina equilibrio secular (se forma tanto Th-230 como
se destruye). Por tanto el método uranio-torio no puede datar más
allá de 500.000 años, aproximadamente.
Esta entrada se publica conjuntamente en Amazings.es y es una participación en la
Edición 3,14159 del Carnaval de Matemáticas que organiza Scientia y en la XVI Edición del Carnaval de Química
que alberga ¡Jindetrés, sal!
Referencia:


No hay comentarios:
Publicar un comentario