Hay ocasiones en las que un artículo científico,
independientemente del interés intrínseco del hallazgo o
comprobación que describe, pone de manifiesto cómo las
simplificaciones que se hacen, incluidas las de los libros de texto,
al intentar hacer comprensibles las ideas científicas tienen el
efecto de que después sea mucho más difícil entender nuevos
desarrollos. A éstos se les suele llamar contraintuitivos. Una de
los conceptos más recurrentes entre los afectados es el de entropía
y, por extensión, el de orden.
Un artículo publicado en Science por el equipo encabezado
por Pablo Damasceno, de la Universidad de Michigan en Ann Arbor
(EE.UU.), nos recuerda que ni la entropía, ni los procesos
termodinámicos espontáneos, están relacionados per se con
lo que intuitivamente entendemos por desorden. La entropía está
relacionada con el número de “posibilidades” para un sistema, lo
que muchas veces se traduce en “desorden” pero, como muestra esta
investigación, no siempre.
Y es que la naturaleza no entiende de orden o desorden, que son
conceptos puramente de la mente humana en su afán por hacer
inteligible el entorno. La naturaleza entiende de minimización de la
energía y maximización de posibilidades.
Pero vayamos por partes.
La organización espontánea de
distintas unidades elementales en estructuras ordenadas se encuentra
en todas las escalas. Ejemplos evidentes son los cristales a nivel
atómico, los cristales plásticos y líquidos a nivel molecular o
las superceldillas de nanopartículas o los coloides. En ciencia de
materiales es crítico conocer la relación entre las ordenaciones y
sus constituyentes ya que las propiedades físicas de aquellas
dependen en gran manera de la estructura.
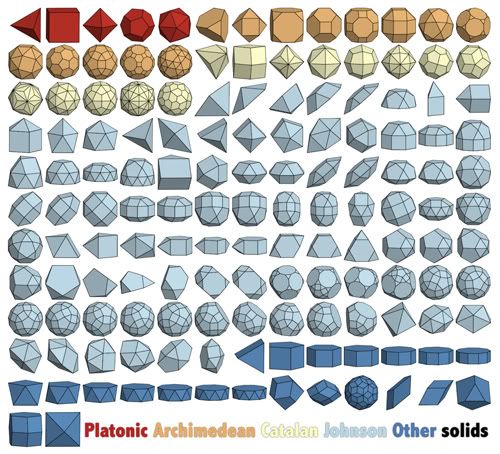
Lo que han conseguido Damasceno et
al. mediante simulaciones por ordenador es poder predecir las
estructuras que formarán partículas de distintas formas, en
concreto 145 poliedros convexos distintos. De hecho, los autores
demuestran que la forma en que se orientan depende sólo de su forma
anisótropa. Pero, y esto es lo que consideramos interesante
resaltar, este estudio demuestra también que existe una llamativa
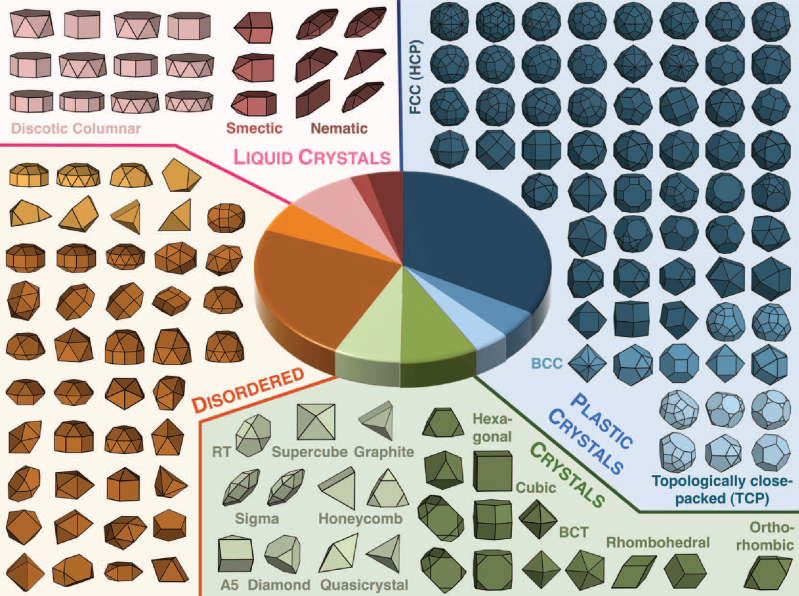
tendencia a la auto-organización y a la diversidad estructural. Es
decir, que haciendo mediciones simples de la forma de la partícula y
el orden local (orden a corto) en un fluido se puede predecir si esa
forma se organizará espontáneamente como un cristal líquido, como
un cristal plástico, como un cristal en sentido estricto o si no se
organizarán en absoluto.
Pero, ¿cómo se forman estructuras ordenadas espontáneamente?
Muy fácil, diréis algunos, el sistema se enfría, formándose las
estructuras ordenadas y la entropía del universo aumenta aunque la
del sistema disminuya. Pero, no. No existe variación de temperatura.
Tal y como están planteadas las simulaciones, partículas sólidas
que no interactúan más allá de su geometría, no existe variación
energética, tan sólo maximización entrópica. Nos explicamos.
Sabemos por la segunda ley de la termodinámica que, todo lo demás
constante, el sistema evolucionará espontáneamente hacia la
configuración que consiga el máximo incremento en la entropía.
Habitualmente, como decíamos más arriba, esto coincide con el
máximo desorden. Así, un libro de texto puede decir que “los
sistemas evolucionan espontáneamente en el sentido en el que aumenta
el desorden”, en abierta contradicción con lo que vemos aquí.
La clave está en el espacio disponible. Si las partículas
tuviesen todo el espacio del mundo no cabe duda de que se
dispersarían tomando posiciones al azar. Pero si el espacio es muy
limitado la cosa cambia. En estas circunstancias las posibilidades
distintas de acoplamiento aumentan si las partículas se orientan
cara a cara, lo que nosotros interpretamos como orden.
Dado que la eficiencia en el empaquetamiento aumenta con el área
de contacto, la ordenación puede ser interpretada como el resultado
de una fuerza entrópica efectiva, direccional y multicuerpo. Esta
fuerza aparece a partir del mayor número de configuraciones
disponibles para el conjunto del sistema, lo que trae como
consecuencia que los poliedros con un número adecuado de caras se
ordenen de determinada manera. Esta idea de fuerza entrópica
direccional es la que sugiere que la forma de las partículas puede
usarse para predecir las estructuras.
No es que el desorden (entropía) cree orden. Es una cuestión de
opciones disponibles: en este caso las disposiciones ordenadas son
las que producen el máximo número de posibilidades. Pero no hay que
circunscribirse al mundo nanoscópico. Este fenómeno es conocido
para cualquiera que haya trasladado una caja de naranjas (de esferas
en general): si se agita tiende a ordenarse.
Por ello esta sería una buena ocasión para abandonar esa
aproximación a la entropía como desorden y empezar a asimilar la
definición estadística de la entropía, mucho más útil a la larga
aunque menos intuitiva para algunos al principio: la entropía de un
sistema es proporcional* al número de estados posibles en los que
puede estar.
Volviendo a los resultados de Damasceno et al., de los 145
poliedros estudiados el 70 por ciento produjeron estructuras
cristalinas de algún tipo. Algunas de estas estructuras eran
realmente complejas, con hasta 52 partículas en el patrón que se
repetía.
Como siempre con un hallazgo interesante, estos resultados nos
sugieren muchas más preguntas. La más inmediata es ¿por qué el 30
por ciento no forma estructuras ordenadas quedándose con estructura
vítrea (de vidrio)? ¿Por qué se resisten al orden? Un hilo
misterioso del que tirar.
[*] En sentido estricto proporcional logarítmicamente: S = k ln W donde S es entropía, W el número de estados accesibles del sistema y k una constante (de Boltzmann). Esta es la forma de Planck de la ecuación de Boltzmann.
Esta entrada es una participación de Experientia docet en la XVII Edición del Carnaval de Química que organiza Un geólogo en apuros.
[*] En sentido estricto proporcional logarítmicamente: S = k ln W donde S es entropía, W el número de estados accesibles del sistema y k una constante (de Boltzmann). Esta es la forma de Planck de la ecuación de Boltzmann.
Esta entrada es una participación de Experientia docet en la XVII Edición del Carnaval de Química que organiza Un geólogo en apuros.
Referencia:
Damasceno PF, Engel M, & Glotzer SC (2012). Predictive self-assembly of polyhedra into complex structures. Science (New York, N.Y.), 337 (6093), 453-7 PMID: 22837525


Me ha gustado mucho el post. Siempre he tenido un poco de lío con el concepto de "entropía", y creo (tengo que re-pensarlo) que gracias a lo que he leído hoy lo entiendo mejor. Muchas gracias!!!
ResponderEliminarEstimado César, la noticia es interesante, pero en mi opinión el titular lleva a engaño. La entropía no es desorden... en un sistema con un espacio limitado. Es esta condición del espacio limitado la que determina la aparición de redes cristalinas. Yendo al extremo, en un espacio limitado de dos metros cúbicos, sólo hay una forma de que quepan dos cubos de un metro cúbico cada uno y es enfrentado sus caras. Saludos cordiales.
ResponderEliminarexelente post. pero el ejemplo de las naranjas tiene truco: una parte de la ordenación bene por disminucíndinución de la energía (temperatura). esta contribución es significativa en el caso de tener varios pisos ya que las zonas entre naranja y naranja es´tan más bajas queel resto, con lo que parte de la ordenación estaría relacionada con la disminución de la energía (temperatura). El experimento más sencillo cercano al contado en el post sería tener un sólo piso de naranja (o dados) en la caja (así el esta inicial y el final podrían tener la misma energía),pero:
ResponderEliminar-ni muy lleno (que no se puedan mover las naranjas)
-ni muy vacío (donde aparecen estado en los que la naranjas están tan separadas que es dificil apreciar un orden)
Una buena entrada, aunque según para que niveles no cabe duda que relacionar la entropía con el desorden es lo más fácil para darla a conocer a las nuevas generaciones. De todas formas, hay que explicar las cosas como son.
ResponderEliminarUn Saludo
"Entre todos Química Más Fácil"