Frans de Waals: El comportamiento moral de los animales

El pasado viernes Antonio Osuna (BioTay) publicaba en el Cuaderno de Cultura Científica de la UPV/EHU un magnífico artículo titulado El origen natural del bien. En él explicaba cómo el altruismo es algo no exclusivo de los humanos encontrándose ejemplos en el comportamiento de muchos animales. En el vídeo que presentamos a continuación Frans de Waals abunda en esta idea y la amplía al comportamiento moral en animales en sentido amplio.

El vídeo es muy intructivo, divertido e invita a la reflexión y complementa, creemos, perfectamente el texto de BioTay. Está subtitulado en español. ¡Que lo disfrutes!

Incompletitud y medida en física cuántica (V): decoherencia o el papel de la consciencia

Un físico teórico puede distinguirse de un matemático de varias maneras. Quizás la más inmediata sea que el primero tiene la intención de que sus ecuaciones en última instancia reflejen una parte del funcionamiento del universo, mientras que las del segundo están autocontenidas. Podríamos incluso ir más allá y decir que, por este hecho, los físicos necesitan interpretar físicamente sus matemáticas, dotarlas de un sentido físico, racionalizador, que haga al mundo pensable, lo que podría argumentarse que surge de su propia condición de humanos. Y también en esto la física cuántica es extraña.

Esta necesidad de dotar de sentido físico a la mecánica cuántica se traduce en la adopción, consciente o no, de una interpretación de la misma cuando se transmite, ya sea en la enseñanza o en la comunicación de resultados o en los libros de texto. La necesidad de un lenguaje común, la presión de estandarización en un mundo global, hace que una interpretación de la mecánica cuántica sea la predominante, la llamada de Copenhague. El que esta interpretación en concreto tenga esta posición de privilegio por una magnífica campaña de marketing es un tema muy interesante de sociología de la ciencia pero que no corresponde discutir ahora. Lo que quizás si debamos mencionar es que muchos físicos no se salen de ella y llegan a negar cualquier otra interpretación como fantasía (llegando a afirmar que ellos no hacen filosofía, sino física, cuando en realidad lo que hacen es renunciar a pensar, pero esa es otra cuestión).

Lo paradójico y llamativo es que considerar la mecánica cuántica como completa y defender la interpretación de Copenhague como la canónica es una misión de corto recorrido. En cuanto se explora mínimamente nos encontramos con indefiniciones, inexactitudes e incongruencias. Tanto es así, que sin salirnos de Copenhague (término que usaremos como paraguas), podemos hablar de tres grupos de interpretaciones estándar fijándonos tan sólo en dos criterios y usando al gato deSchrödinger como piedra de toque. Esos dos criterios son a) qué consideramos como ente cuántico y b) qué consideramos medida.

Antes de explorar brevemente los tres grupos de interpretaciones conviene recordar un par de cosas que explican nuestra elección de criterios. En primer lugar, de acuerdo con Copenhague, la razón por la que no podemos decir qué atributos tiene un ente cuántico antes de la medida no es simplemente porque no sepamos cuáles son. Sino que no podemos decir cuáles son porque no existen antes de medir, esto es, no existe una realidad profunda e independiente consistente en objetos con atributos definidos existentes antes de la medición de los mismos (para ser precisos los entes cuánticos sí tienen unos atributos antes de ser medidos, los llamados atributos estáticos, como la masa; pero esto no influye en el razonamiento).

En segundo, esto no significa que Copenhague niegue la existencia de la realidad: existe un electrón por ahí, existen entes cuánticos en general, pero algunas de sus características no las puedo conocer hasta de que mida. Dicho esto, veamos cómo interpretan la realidad cada uno de los tres grupos de interpretaciones.

Continúa leyendo en el Cuaderno de Cultura Científica

Curiosity descubre un gradiente redox en Yellowknife Bay

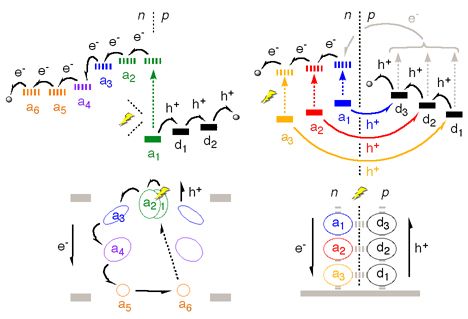
Esquema de gradientes redox biológicos terráqueos

El pasado día 12 saltaba la noticia: “Marte pudo haber albergado vida alguna vez, según la NASA” (ABC), “El 'Curiosity' demuestra que pudo haber vida en Marte” (Materia), “La NASA confirma que Marte pudo haber albergado vida” (Medciencia), son algunos ejemplos. Si lees estas noticias te darás cuentan de que, como solemos decir, tocan de oído. Primero porque se quedan con el chascarrillo de John Grotzinger, director de la misión MSL-Curiosity, en la rueda de prensa: “El agua de Marte del pasado habría sido potable”; segundo porque confunden churras con merinas o, en este caso, minerales con elementos químicos: “Entre los minerales hallados hay azufre, nitrógeno, hidrógeno, oxígeno y fósforo” y, tercero, porque o no pasan o pasan de puntillas y mal por el descubrimiento mayor. Para empezar la composición elemental cualitativa no es una novedad, el que haya arcillas tampoco, ni siquiera la presencia de agua es algo novedoso. Entonces ¿qué se ha encontrado realmente que amerite el calificativo de “habitable” para el Marte del pasado? La respuesta es una palabra no demasiado habitual al hablar de Marte: un gradiente; para ser exactos, un gradiente redox. Vamos a ver qué es esto.

Como asumo conocidos los antecedentes, nos concentraremos en lo que nos interesa ahora. Curiosity taladró una roca en un área llamada Yellowknife Bay, que parece que es probable que sea la desembocadura de un antiguo sistema fluvial o bien el lecho de un lago intermitente. El material triturado del interior de la roca fue analizado usando varias técnicas, entre ellas difracción de rayos X de polvo (para los aficionados a la cristalografía, la DRXP de toda la vida) y cromatografía de gases (para los aficionados a C.S.I., el aparato objeto de los video-clips musicales de la serie).

El análisis puso de manifiesto que la roca era una lutita (roca sedimentaria constituida por detritos) de grano fino que contenía varios minerales ígneos, entre ellos olivino, un silicato de hierro y magnesio (su nombre viene de su color verde oliva, como bien saben los visitantes y lugareños de las Islas Canarias, especialmente Lanzarote). Lo más importante es que aproximadamente un 20% de la muestra consistía en minerales arcillosos. Las lutitas cambian de color en función del ambiente en el que estén: son grises, o grises verdosas, dependiendo de la composición, en ambientes reductores y rojas o amarillentas en ambientes oxidantes. La muestra era grisácea por lo que la arcilla detectada es el producto de la reacción de los detritos ígneos con agua neutra y con bajo contenido en sales (de aquí lo del “agua potable” de Grotzinger).

Por otra parte la presencia de sulfato de calcio en las muestras sugiere que el terreno circundante es o neutro o ligeramente alcalino. Pero hay más indicios de que el entorno no es oxidante en exceso. Así lo demuestran la existencia del mismo elemento en distintos estados de oxidación: por ejemplo, el azufre está como sulfato y como sulfuro. Y esto es lo importante, ya que significa que en Marte al menos hay un lugar en el que existe un gradiente redox.

Todas las reacciones metabólicas que conocemos son reacciones redox, esto es, de oxidación-reducción. En otras palabras, cada reacción que produce energía en un ser vivo  requiere de un oxidante (una especie química capaz de captar electrones) y un reductor (otra especie capaz de cederlos). A su vez los productos de esta reacción, oxidados y reducidos, pueden participar en reacciones subsiguientes. El hecho de que se haya encontrado en Yellowknife Bay elementos en distintos estados de oxidación a la vez y en el mismo lugar, indica que podrían existir reacciones que tuviesen a estas especies como reactivos/productos como parte del metabolismo de una vida microbiana (de aquí lo de “apto para que vivieran microbios”).

Hasta aquí vemos que el Marte rojo y fuertemente oxidante, con percloratos que acaban con lo que se mueva, se ve transformado en un Marte gris, mucho más amigable, en el pasado, para la existencia hipotética de posibles formas de vida no extremófila según los estándares terráqueos (de aquí lo de “habitable en el pasado”).

Recapitulando, lo que tenemos es presencia en el pasado de agua líquida no salina con elementos en diferentes estados de oxidación y carbono en distintas formas. Esto podría (ojito al condicional) ser interpretado de la siguiente manera: tenemos un medio (agua) en el que una estructura orgánica (carbono) tendría a su disposición una fuente de energía en forma de gradiente redox (elementos en distintos estados de oxidación).

Lo que antecede ya es bastante espectacular como para tener la necesidad de afirmar “que pudo haber vida”, cuando no hay indicio alguno de que la haya habido. Esta afirmación es del tipo de “yo pude haber sido monja clarisa” referida a Lady Gaga, no hay pruebas ni de que se lo hubiese planteado, por lo que es pura propaganda; el título de esta entrada es mucho menos llamativo pero más acorde con la realidad.

Esta entrada es una participación de Experientia docet en la XXIII Edición del carnaval de Química que organiza Moles y Bits.

Incompletitud y medida en física cuántica (IV): un gato y el destino del universo

Cuando se estudia el concepto de vida media de los materiales radioactivos suele haber más problemas con su sentido matemático que con sus implicaciones filosóficas para nuestra visión de la realidad. Quizás porque el estudiante ya está acostumbrado a que a nivel atómico ocurren cosas extrañas. En cualquier caso repasémoslo someramente para un caso muy concreto.

Imaginemos que tenemos una cantidad del isótopo neptunio-231. Este isótopo tiene una vida media de 48 minutos, lo que quiere decir que si empezamos con una cantidad dada, 48 minutos después la mitad de esa cantidad se habrá desintegrado, esto es, tendremos la mitad de la cantidad original de neptunio-231 y los productos de descomposición de la otra mitad. Hasta aquí no debería haber mayor problema. Pero, ¿qué ocurre si empezamos con un sólo átomo?¿Qué tendremos después de 48 minutos?

Aquí nuestra aproximación debe cambiar. Donde antes teníamos la certeza práctica de que obtendríamos la mitad de los átomos de partida sin desintegrar ahora tenemos que hablar de probabilidades. Efectivamente, tenemos una probabilidad del 50% de que tras 48 minutos nuestro átomo de neptunio-231 se haya desintegrado, pero como está gobernado por la ecuación de Schrödinger, sólo sabremos su estado cuando hayamos medido. Es decir que, mientras no midamos, el átomo se encuentra en un estado de superposición desintegrado/no-desintegrado.

Mientras esta indefinición se mantenga constreñida al ámbito de lo muy pequeño podemos sentirnos cómodos y continuar con nuestro día a día como si tal cosa. Pero no existe nada en la mecánica cuántica que impida que esta indefinición infecte nuestro mundo macroscópico. El primero que nos consta que se dio cuenta fue Albert Einstein. Tras la publicación de su artículo con Podolsky y Rosen (véase Los dados de dios) se intensificó su correspondencia con ciertos físicos, entre ellos Schrödinger, en la que expresaban sus preocupaciones por lo que veían como deficiencias de la teoría cuántica. En una carta a Schrödinger fechada el 8 de agosto de 1935 proponía un “crudo ejemplo macroscópico”:

El sistema es una sustancia en un equilibrio inestable, quizás un montón de pólvora que, por medio de fuerzas internas, podría arder espontáneamente, y donde la vida media de todo el montaje sea de un año. En principio esto podría representarse mecano-cuánticamente muy fácilmente. Al comienzo la función ψ caracteriza un estado macroscópico razonablemente bien definido. Pero, según tu ecuación [de Schrödinger], esto no es así transcurrido un año. Más bien la función ψ describe entonces una especie de mezcla de sistemas ya-explotado y aún-no-explotado. No hay forma de interpretación que permita que esta función ψ se convierta en una descripción adecuada del estado real del asunto; [ya que] en realidad no existe intermedio entre ya-explotado y no-explotado.

Puede que inspirado por esta idea [no lo sabemos porque Schrödinger no cita a Einstein, algo que terminó por convertirse en costumbre, véase a este respecto nuestro Einsteiny...Erwin Schrödinger], Schrödinger plantearía en un artículo titulado “La situación actual de la mecánica cuántica” publicado el 29 de noviembre de 1935 en Die Naturwissenchaften el que probablemente sea uno los experimentos mentales más famosos de todos los tiempos, en estos términos:

Uno puede incluso construir ejemplos ridículos. Un gato está encerrado en una cámara de acero, junto con la siguiente máquina infernal (que uno debe asegurar contra el acceso directo del gato): en el tubo de un contador Geiger hay una pequeña cantidad de material radioactivo, tan pequeña que aunque uno de sus átomos podría desintegrarse en el curso de una hora, es igualmente probable que ninguno lo haga. Si la desintegración tiene lugar, el contador se dispara y por medio de un relé hace que un pequeño martillo se ponga en movimiento y haga añicos una pequeña botella de ácido prúsico [cianuro de hidrógeno]. Cuando el sistema entero se deja sólo una hora, uno diría que el gato está aún vivo si en el intervalo ningún átomo de ha desintegrado. La primera desintegración atómica lo habría envenenado. La función ψ de todo el sistema daría una expresión para todo esto en la que, en igual medida, el gato vivo y el gato muerto (sit venia verbo [permítaseme la expresión]) se mezclan o emborronan.

Sigue leyendo en el Cuaderno de Cultura Científica

Aprendiendo a controlar un nuevo cuerpo

Los avances en los estudios de las interacciones entre encéfalo y máquinas son mucho más espectaculares de lo que quizás te puedas imaginar. En el siguiente vídeo Miguel Nicolelis, de la Universidad de Duke, explica cómo hace diez años un chimpancé aprendió a tener un tercer brazo. El año pasado era capaz de controlar un cuerpo 5 veces el tamaño del suyo. Antes había aprendico a manejar un avatar y a reconocer señales eléctricas como correspondientes a la textura de los objetos que veía en una pantalla.

Las implicaciones prácticas del trabajo de Nicolelis son inmediatas: uno de sus objetivos es que un niño tetrapléjico realice el saque de honor en la Copa del Mundo de Brasil-2014 manejando un exoesqueleto con la mente. Las filosóficas también: los límites de lo que llamamos nuestro cuerpo ya no es la piel, ni la distancia es tampoco un límite. 

El vídeo aún no tiene subtítulos en español, aunque sí en inglés, y Nicolelis, como brasileño que es, pronuncia el inglés cuidadosamente. Haz un esfuerzo, lo merece.

El universo en un día

SÁBADO 25 DE MAYO 2013 – Paraninfo de la Universidad del País Vasco en Bilbao

SESIÓN DE MAÑANA

9:45 – Presentación e inauguración del evento.

10:00 – El Big Bang – Miguel Santander (Astrofísico y escritor de ciencia ficción)

10:30 – Las primeras galaxias – Javier Armentia (Astrofísico y director del Pamplonetario)

11:00 – La vida de las estrellas – Natalia Ruiz (Divulgadora científica)

11:30 – Descanso

12:00 - Formación del sistema solar – Ricardo Hueso  (Profesor en la ETS de Ingeniería y miembro del Grupo de Ciencias Planetarias de la UPV/EHU)

12:30 – El nacimiento de la Tierra – César Tomé (Divulgador científico)

13:00 – El origen de la vida – Carlos Briones (Científico del CSIC en el Laboratorio de Evolución Molecular del Centro de Astrobiología CAB-INTA)

13:30 – Descanso

SESIÓN DE TARDE

17:00 – La evolución – Antonio Osuna "Biotay" (Divulgador científico)

17:30 – Vida y diversidad – Carlos Chordá (Divulgador científico)

18:00 – Los inicios del hombre – Pepe Cervera (Paleontólogo y divulgador científico)

18:30 Descanso

19:00 – Naturaleza y cultura humana – Juan Ignacio Pérez (Coordinador de la Cátedra de Cultura Científica UPV/EHU)

19:30 – El futuro de la Humanidad – Gouki (Divulgador científico)

20:00 – El final del Universo – Aitor Bergara (Profesor de Física de la Universidad del País Vasco y miembro del Centro de Física de Materiales – CSIC-UPV)

La entrada, como de costumbre, será gratuita hasta completar el aforo.

Incompletitud y medida en física cuántica (III): entrelazamientos y desigualdades

La conferencia Solvay de 1927 es conocida, entre otras cosas, por las intensas discusiones entre Einstein y Bohr. Einstein solía proponer un experimento mental que contradecía algún punto de la mecánica cuántica por la tarde, solo para que Bohr apareciese con una solución por la mañana. La conferencia terminó con una derrota del bando de Einstein que, además, se vio manifiestamente diezmado en el número de miembros.

Pero aquello fue sólo una batalla para Einstein. El artículo de 1935 con Podolsky y Rosen, fue un fuerte contraataque a la línea medular de la interpretación de Copenhague de la mecánica cuántica. Un contraataque que costó más de treinta años neutralizar adecuadamente y cuyo desenlace no vieron ni Einstein (muerto en 1955) ni Bohr (en 1962).

La conclusión del artículo de Einstein, Podolsky y Rosen, esto es, que la mecánica cuántica estaba incompleta y existen variables locales ocultas (véase la segunda parte de esta serie) pasó a ser conocida como paradoja EPR. Sin embargo, un comentario de Erwin Schrödinger en una carta a Einstein nos daría un término posiblemente más familiar, Verschränkung, lo que hoy conocemos como entrelazamiento, “para describir las correlaciones entre dos partículas que interactúan y entonces se separan, como en el experimento EPR”. El propio Schrödinger elaboraría su idea publicando un artículo con Max Born en 1935 titulado “Discusiones sobre las relaciones de probabilidad entre sistemas separados”. En este artículo encontramos lo que ya expusimos en la primera parte, a saber:

“Yo no llamaría [al entrelazamiento] un sino el rasgo característico de la mecánica cuántica, el que fuerza su separación completa de las líneas clásicas de pensamiento.”

En ningún lugar es esto más evidente que en el propio artículo EPR. Efectivamente, por primera vez en la historia de la física los autores sienten la necesidad de definir “realidad física” [traducción propia]:

“Si, sin perturbar el sistema de ninguna manera, podemos predecir con certeza el valor de una magnitud física, entonces existe un elemento de realidad física correspondiente a esta magnitud física”

Dicho con otras palabras: si una propiedad física de un objeto puede ser conocida sin que éste sea observado, entonces esa propiedad no ha podido ser creada por la observación. Si no fue creada por la observación debe haber existido como realidad física antes de su observación. Citando de nuevo a Einstein:

“Me gusta pensar que la Luna sigue ahí incluso cuando no la estoy mirando”

El realismo local, esto es, la combinación del principio de localidad (un objeto se ve influido solamente por su entorno inmediato) y la asunción realista de que todos los objetos deben objetivamente tener un valor pre-existente de cualquier posible variable objeto de medida antes de que la medida se realice, está en el corazón de la mecánica clásica, de la relatividad general y de la electrodinámica. Es el realismo local lo que Einstein, Podolsky y Rosen usan en su paradoja y lo que entra en contradicción con el entrelazamiento cuántico, y cuya salvaguarda apuntaría a la existencia de variables locales ocultas.

Estaba claro que la teoría se encontraba atascada en este punto. Sólo la experimentación podía cortar este nudo gordiano. Pero, ¿habría alguna forma de comprobar experimentalmente la existencia de estas variables ocultas? Pues sí, pero habría que esperar a otro desarrollo teórico. John Bell presentó en 1964 en su artículo “Sobre la paradoja EPR” un teorema que permitía diseñar experimentos para comprobar la existencia o no de estas variables ocultas. Este teorema, habitualmente llamado la desigualdad de Bell, relativamente poco conocido, ha sido calificado como el “descubrimiento más profundo de la ciencia” (no de la física, sino de la ciencia). Los diseños experimentales basados en él apuntan a que el realismo local es violado por la mecánica cuántica.

Sigue leyendo en el Cuaderno de Cultura Científica

Olas con forma de estrella.

El océano puede producir un tipo exótico de ondas llamado ola gigante cuando las olas normales se combinan de determinada manera. En el siguiente vídeo vemos un ejemplo en un tanque de ensayo.

Estos patrones de ondas pueden, teóricamente, adoptar diferentes formas, pero el caso es que en el laboratorio sólo se han reproducido unas pocas. Ahora, un equipo de investigadores encabezado por Jean Rajchenbach, de la Universidad de Niza (Francia), han conseguido producir ondas estacionarias con formas poligonales y de estrella agitando verticalmente un recipiente lleno de aceite líquido. Los resultados se publican en Physical Review Letters.

A las olas oceánicas, y a ondas similares en fluidos, se las llama ondas de gravedad (no se confunda con onda gravitacional) porque la principal fuerza restauradora es la gravedad. Las ecuaciones básicas que describen estas olas son no lineales, lo que viene a significar que ondas de diferente longitud de onda pueden interaccionar entre sí y, bajo ciertas condiciones, formar patrones poco habituales, como los solitones (ondas solitarias de larga duración), con forma de U y con forma de X. Estas formas raras a veces tienen equivalentes en óptica o en la física de los átomos superenfriados.

Para explorar nuevas posibilidades no lineales, los investigadores colocaron una fina capa de aceite de silicona en un recipiente plano y lo agitaron arriba y abajo a un ritmo de 10 veces por segundo. Al inicio observaron ondas estacionarias simétricas circularmente pero cuando incrementaron la amplitud de la agitación, las crestas de las olas formaron aristas y vértices de, alternativamente, estrellas de cinco puntas y pentágonos. Variando la profundidad del fluido y los parámetro de la agitación produjeron otras combinaciones estrella-polígono con tres, cuatro y seis lados. Sin embargo, la forma del recipiente no era un factor, ya que se formaban patrones idénticos tanto en recipientes circulares como rectangulares. Las formas que se observan se pueden explicar teóricamente por la interacción resonante no lineal de tres ondas diferentes generadas por la agitación.

Referencia:

Rajchenbach, J., Clamond, D., & Leroux, A. (2013). Observation of Star-Shaped Surface Gravity Waves Physical Review Letters, 110 (9) DOI: 10.1103/PhysRevLett.110.094502

Incompletitud y medida en física cuántica (II): los dados de dios

La mecánica cuántica moderna tiene fecha y lugar de nacimiento conocidos, Isla de Helgoland, en la costa de Alemania, junio de 1925. Fue en este lugar y fecha que Werner Heisenberg elaboró el germen de la teoría matricial de la mecánica cuántica. Al año siguiente, en 1926, aparecería una forma que se demostró equivalente, la que conocemos como ecuación de Schrödinger.

El supervisor de Heisenberg en Gotinga, Max Born, escribió a Einstein informándole del hallazgo: “parece muy místico, pero ciertamente es correcto y profundo”. Einstein, a pesar de sus propias contribuciones al desarrollo de la teoría cuántica, no terminaba de aceptar el planteamiento. Cuando el propio Born en 1926 interpretó el cuadrado de la función de onda, la función solución de la ecuación de Schrödinger, como la probabilidad de encontrar la partícula en un determinado lugar, aquello llegó a un extremo que Einstein no podía soportar. El 4 de diciembre de 1926 escribía a Born un comentario que después se ha hecho famoso [traducción y énfasis nuestros]:

La mecánica cuántica es ciertamente imponente. Pero una voz interior me dice que no es todavía la auténtica. La teoría dice mucho, pero no nos aproxima un ápice al secreto del “viejo”. Yo, en cualquier caso, estoy convencido de que él no lanza dados.

Einstein con esta expresión lo que le está diciendo a Born es, ni más ni menos, que la teoría está muy bien pero que, desde su punto de vista, está incompleta. Esta incomodidad de Einstein con la probabilidad (“él no tira dados”) es a veces incomprendida, incluso por muchos hoy día, casi un siglo después, porque no se tiene una idea clara de a qué se refiere esta probabilidad. Einstein se sentía más que cómodo con la física estadística, por lo tanto no es un problema de herramienta sino de significado.

En esa época andaba por Gotinga un joven inglés retraído que preparaba notas para lo que en 1930 sería uno de los libros fundamentales sobre la mecánica cuántica, todavía en uso hoy día, Principles of Quantum Mechanics. Dejemos que sea Paul A.M. Dirac el que nos explique el matiz que tanto incomodaba a Einstein (y a otros tantos, entre ellos Schrödinger o de Broglie).

Continúa leyendo en el Cuaderno de Cultura Científica